A barra fina de 4 kg é suportada horizontalmente por uma mola em A e uma corda em B. Determine a aceleração angular da barra e a aceleração do centro de massa da barra no instante que a corda em B é cortada. Dica: a rigidez da mola não é necessária para o cálculo.
Passo 1
Vamos considerar a aceleração da gravidade como .
Usaremos a ilustração a seguir para nos ajudar aplicar as equações de movimento para o sistema:
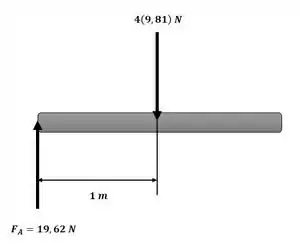
Vamos inicialmente calcular a reação no ponto A, pois uma vez que a deflexão na mola não muda, a força de reação também não irá mudar:
Passo 2
Agora, iremos propor as equações do movimento do sistema na direção x e na direção y:
Logo:
Passo 3
Agora, iremos aplicar o somatório de momentos em torno do centro de massa da barra: