Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas fundamentais - Ex. 2
A barra fina uniforme de 25 kg é submetida a um momento de binário M = 150 N.m. Se a barra está em repouso quando , determine a velocidade angular quando .
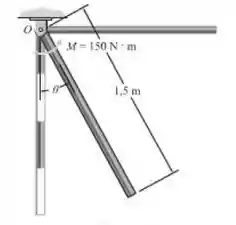
Passo 1
Sabendo que a barra parte do repouso (ω1 =0), ou seja, T1 = 0 , avalia-se a energia cinética para o estágio 2, sabendo que o movimento é plano geral. Assim:
Sabendo que o momento de inércia de massa é dado por:
E, sabendo que a velocidade linear pode ser escrita por meio da angular da seguinte forma:
Passo 2
O trabalho será quantificado devido ao momento aplicado à roda somado aquele desenvolvido pelo peso da barra, assim, pelo princípio do trabalho e energia, tem-se que:
Resposta
A velocidade angular para a inclinação de 90 será de 2,35 rad/s.
Exercícios de Livros Relacionados
Os dois rebocadores exercem uma força de intensidade F cada uma, sobre o navio de massa m e raio de giração kg, que estão sempre direcionadas perpendicularmente a linha central do navio. Determinar su
O motor elétrico apresentado está fornecendo 4k W a 1725r p m para uma bomba a qual aciona. Calcule o ângulo δ por meio do qual o motor se inclina sob a ação da carga, se a rigidez de cada uma de suas
A respeito do conjunto apresentado, o braço O A possui uma massa de 0,8k g e um raio de giração em relação a O de 140m m . A engrenagem B tem uma massa de 0,9k g e pode ser tratada como um disco circu
Sob intenso desenvolvimento está o armazenamento de energia em discos que giram em alta velocidade onde o atrito é efetivamente eliminado pelo encapsulamento do rotor em um compartimento sob vácuo e u
Para a haste delgada articulada de comprimento l , determine a distância x para a qual a velocidade angular será máxima quando a barra passar pela posição vertical, após ter sido liberada na posição h