Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas fundamentais - Ex. 3

A barra fina uniforme de 50 kg está em repouso na posição mostrada, quando P= 600N é aplicada. Determine a velocidade angular da barra quando ela atinge a posição vertical.

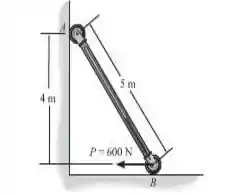
Passo 1

Sabendo que a barra parte do repouso ( ω 1 = 0 ), ou seja, T 1 = 0 , avalia-se a energia cinética para o estágio 2, sabendo que o movimento é plano geral. Assim:

T 2 = 1 2 m V 2 + 1 2 I G ω 2 2

Sabendo que o momento de inércia de massa é dado por:

I G =   1 12 m × L ²

Onde L é o comprimento da barra.

I G =   1 12 × 50 × 5 ²

I G =   104,17   k g . m ²

E, sabendo que a velocidade linear pode ser escrita por meio da angular da seguinte forma: V =   r × ω , explicitando que o r é a metade da barra, pois a barra gira.

T 2 = 1 2 × 50 × 2,5 × ω 2 ² + 1 2 × 104,17 × ω 2 2

T 2 = 208,33   ω 2 2

Passo 2

O trabalho será quantificado devido a força P à roda somado aquele desenvolvido pelo peso da barra, assim, pelo princípio do trabalho e energia, tem-se que:

T 1 +   ∑ U 1 → 2   =   T 2

0 + ( P × s p + ( -   W y G ) ) = 208,33 ω 2 2

600 × 3 -   50 × 9,81 × 2,5 - 2 = 208,33 ω 2 2

1800 - 245,25 =   208,33 ω 2 2

ω 2 = 2,73   r a d / s

Resposta

A velocidade angular para quando a barra atinge a posição vertical será de 2,73 rad/s.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O volante de 50k g tem um raio de giração k - = 0,4m , em relação à linha central de seu eixo e está submetido ao torque M = 2 1 - e - 0,1 θN ∙ m , onde θ está em radianos. Se o volante está em repous
O disco uniforme de 6k g gira livremente em relação a um eixo horizontal através de O . Uma barra esbelta de 2k g é fixada ao disco conforme indicado. Se o sistema é levemente deslocado do repouso enq
A alavanca O A de 5,5k g com 250m m de raio de giração em relação a O está inicialmente em repouso na posição vertical ( θ = 90 ° ), onde a mola anexa de rigidez k = 525N / m está sem deformação. Calc
O disco B rola sem deslizar para baixo na inclinação A , que se desloca com velocidade v . Descreva o trabalho realizado pelas forças normal e de atrito que atuam sobre o disco para os casos (a) v = 0
O disco semicircular de massa m = 2k g está montado no aro leve de raio r = 150m m e é liberado a partir do repouso na posição (a). Determine a velocidade angular ω do aro e a força normal N sob o aro