Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 74

A barra fina uniforme tem uma massa de 9 kg. Se a mola está distendida quando θ = 0°, determine a intensidade da força reativa exercida sobre a barra pelo pino A quando θ = 45°, se, nesse instante, ω = 6 rad/s. A mola tem uma rigidez k = 150 N/m e sempre permanece na posição horizontal.

Passo 1

Nesse exercício, iremos adotar a aceleração da gravidade como g = 9,81   m / s 2 .

Nesse caso, devemos primeiramente analisar a deflexão da mola quando θ = 45°, sabendo que, para θ = 0°, a deflexão é nula, quando θ = 45°, teremos o comprimento total subtraído da parcela que foi deslocada:

s = 0,8 - 0,8 c o s 45 ° → s = 0,2343   m

Sendo assim, a força na mola é dada por:

F m = k s = 150 0,2343 → F m = 35,15   N

Ainda podemos decompor a aceleração em suas componentes normal e tangencial:

a G n = ω 2 r G = 6 2 0,4 → a G n = 14,4   m / s 2

a G t = α r G = α 0,4

Passo 2

Para nos auxiliar no cálculo do momento de inércia, usaremos a figura a seguir como referência:

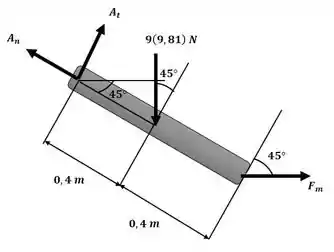
Agora iremos calcular o momento de inércia da barra para posteriormente aplicarmos o somatório de momento em torno do ponto A.

I G = 1 12 m l 2 = 1 12 9 0,8 2

I G = 0,48   k g . m 2

Agora, aplicando o somatório de momento em torno do ponto A, podemos descobrir a aceleração angular α :

↺ + ∑ M A = ∑ M k A

35,15 c o s 45 ° 0,8 - 9 9,81 c o s 45 ° 0,4 = - 9 α 0,4 0,4 - 0,48 α

α = 2,651   r a d / s 2

Passo 3

Agora, usaremos os resultados dos passos 1 e 2 para aplicar o somatório de forças nas direções normal e tangencial e obter o valor das respectivas componentes.

Na direção normal:

+ ↖ ∑ F n = m a G n

A n - 9 9,81 s e n 45 ° - 35,15 s e n 45 ° = 9 14,4

A n = 216,88   N

Na direção tangencial:

+ ↙ ∑ F t = m a G t

9 9,81 c o s 45 ° - 35,15 c o s 45 ° - A t = 9 [ 2,651 0,4 ]

A t = 28,03   N

Com as componentes, podemos calcular o valor do módulo pedido no enunciado:

F A = A t 2 + A n 2 = 28,03 2 + 216,88 2

F A = 218,7   N

Resposta

F A = 218,7   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os elementos de um sistema de controle da orientação angular com volantes de reação para uma nave espacial são apresentado na figura. Oponto G é o centro de massa para o sistema da nave espacial e dos
O disco circular de massa m e raio r está montado na haste vertical com um ângulo α entre seu plano e o plano de rotação da haste. Determine uma expressão para a quantidade de movimento angular H do d
O trem de pouso de uma aeronave, visto de frente, está sendo recolhido imediatamente após a decolagem, e a roda está girando na taxa correspondente à velocidade de decolagem de 200 k m h . A roda de 4
A barra de aço esbelta AB possui uma massa de 2.8 kg e está ligada ao eixo que gira pela barra OG e suas conexões em O e G. O ângulo β permanece constante em 30º, e todo o conjunto rígido gira em torn
O cilindro semicircular maciço de massa m gira em torno do eixo z como uma velocidade angular ω conforme indicado. Determine a sua quantidade de momento angular H em relação aos eixos x-y-z.