Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 121
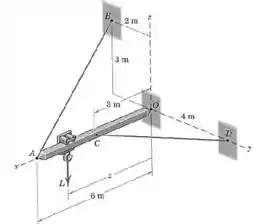
A haste horizontal é sustentada pelos cabos e e por uma rótula em . Para determinar a influência da posição da carga vertical ao longo da haste sobre a reação em , podemos desprezar o peso da haste. Se representa o módulo da força total em , determine a menor razão e o valor correspondente de . Escreva, então, um programa de computador para e trace o gráfico dos resultados para , como uma verificação dos seus cálculos.
Passo 1
Vamos começar escrevendo as trações nos cabos e na forma vetorial. Para isso vamos precisar dos escalares e e dos vetores unitários nas direções de cada um desses.
E vamos também escrever os vetores das posições dos pontos em que cada uma dessas forças atuam:
Além disso temos a força agindo no ponto de posição e a força total agindo em .
Passo 2
Agora vamos usar esses vetores para escrever o momento total do sistema em relação a origem:
E vamos escrever esses produtos vetoriais como determinantes de matrizes:
E agora vamos igualar cada componente a zero:
Passo 3
Agora vamos considerar a condição de equilíbrio das forças agindo em cada direção, lembrando que agora as componentes , e têm que ser levadas em consideração:
Agora é só substituir os resultados que encontramos para e e isolar cada componente de :
E então podemos calcular o módulo de :
Passo 4
Nosso objetivo é encontrar . Isolando na equação de cima ficamos com o seguinte:
E com isso queremos encontrar o valor mínimo de em função de e fazer o gráfico dessa função no intervalo . Vamos começar com o gráfico, que já resolve os dois problemas:
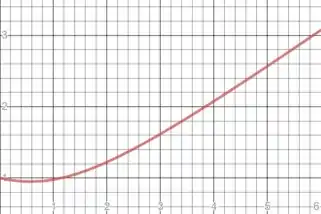
E vamos aproveitar esse gráfico para localizar o ponto de mínimo no intervalo definido:
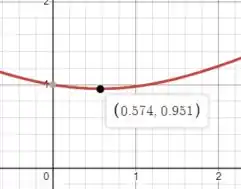
Passo 5
Também podemos encontrar usando métodos de cálculo. Vamos procurar os pontos críticos da função (ou, de forma equivalente, os de ):
Derivando e igualando a zero:
Que é o mesmo resultado de antes.
Resposta
e .