Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 77
A barra OA, que pesa 50 libras com centro de gravidade G, é girada em torno de sua extremidade O e oscila no plano vertical sob a restrição do contrapeso de 20 libras. Escreva a expressão para a energia potencial total do sistema, considerando Vg = 0 quando θ = 0, e calcule Vg como uma função de θ de θ = 0 a θ = 360 ∘. A partir do gráfico dos resultados, determine a posição ou posições de equilíbrio e a estabilidade de equilíbrio em cada posição.
Passo 1
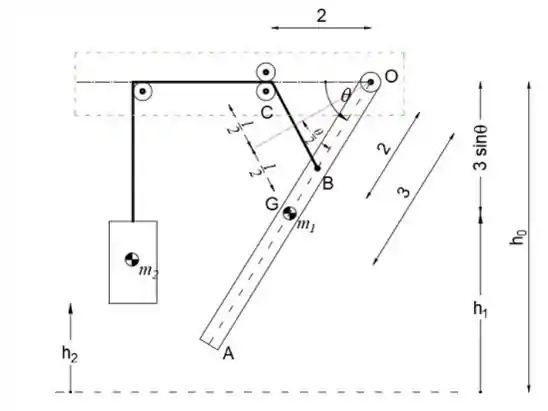
Primeiro, vamos desenhar o diagrama de força ativa
Observe que não há foros externos atuando no sistema, nem molas acopladas. portanto, podemos escrever a equação de equilíbrio como
Podemos ver que quando θ = 0 ∘, os pontos B e C estão sobrepostos, o que significa que o comprimento (BC) ̅ = 0. Se assumirmos que naquele ponto (quando ├ θ = 0 ∘) o peso de 20 lb está no solo, podemos dizer que a altura h_2 é igual ao comprimento do cabo de B a C
Podemos ver pelo esboço que metade do comprimento do cabo é
Portanto, a altura h (comprimento total da mola) é
Uma vez que a altura é
Passo 2
Uma vez que nosso mecanismo contém duas massas, podemos escrever a expressão para a energia potencial gravitacional como
substituiremos e por seus valores, por e por
Uma vez que sabemos que at , podemos determinar a altura ao substituir by 0 e por na equação acima
Portanto,a expressão para energia potencial
Passo 3
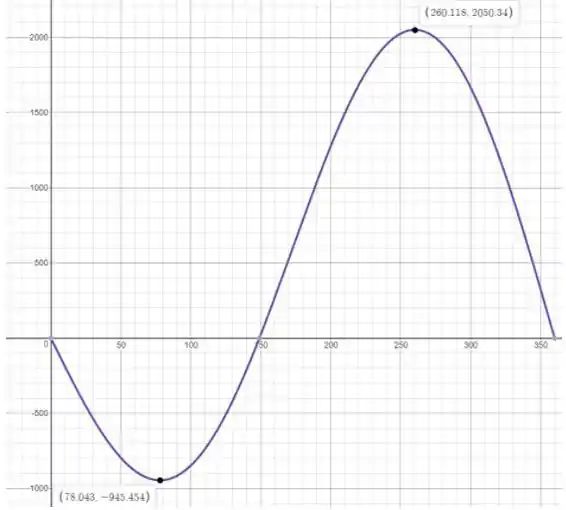
Usando uma calculadora gráfica como o Desmos (link nos comentários), traçaremos a função para Vg no intervalo 0 ∘≤θ≤ 360 ∘
Como o máximo da função está em zero da primeira derivada, podemos dizer que o mecanismo está em equilíbrio em
Observe que, uma vez que a função está aumentando em θ = 78,043 ∘, isso significa que a segunda derivada é maior que zero, ou seja, que o sistema é estável
Observe que, como a função está diminuindo em θ =260,118∘, isso significa que a segunda derivada é menor que zero, ou seja, que o sistema é instável
