Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 50
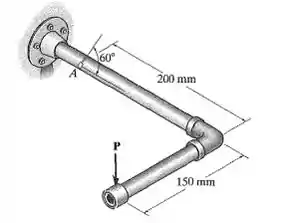
Um extensômetro colocado no plano vertical sobre a superfície externa a um ângulo de 60° em relação ao eixo do tubo dá uma leitura no ponto A. Determine a força vertical P, se o tubo tiver diâmetro externo de 25 mm e diâmetro interno de 15 mm. O tubo é feito de bronze C86100.
Passo 1
Fala aí galera, vamos para mais uma resolução massa do responde aí.
O primeiro passo para resolver este problema é determinar os esforços atuantes:
Podemos ver que a tensão normal em A será 0, pois ele está na linha neutra.
Vamos agora determinar o momento estático, que será dado por:
Com isso, podemos determinar a tensão cisalhante que atuará em A:
Substituindo as variáveis pelos respectivos valores, ficaremos com:
Passo 2
Agora, precisamos calcular a deformação no plano . Para isso, vamos usar a fórmula abaixo:
Como calculamos a tensão cisalhante no primeiro passo e podemos calcular o G, podemos substituir os valores para achar a deformação:
Agora, por fim, podemos calcular o que o problema nos pede, que é o valor de P. Para tal, vamos utilizar a fórmula:
Substituindo os valores e isolando o P, ficaremos com:
Deixando claro que o nosso foco aqui não é treinar contas, mas a teoria. Logo, as operações foram simplificadas.