Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 37
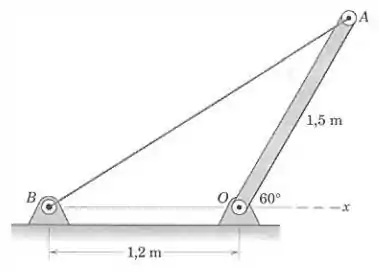
A barra uniforme com é mantida na posição mostrada por um pino liso em e pelo cabo . Determine a força trativa no cabo e o módulo e a direção da reação externa no pino em .
Passo 1
É importante calcularmos o valor do ângulo que o cabo faz com a horizontal:
Sendo assim, somamos todos os momentos em torno de e igualamos a zero:
Passo 2
Através da equação de equilíbrio de forças na horizontal, podemos calcular a componente da força em :
E agora, usando a equação de equilíbrio de forças na vertical, calculamos a componente :
Passo 3
Desse modo, o módulo da reação em será:
E o ângulo com o eixo positivo será:
Resposta
, acima do eixo positivo
Exercícios de Livros Relacionados
5.52. Três livros uniformes, cada um com peso W e comprimento a , são empilhados como na figura. Determine a distância máxima d que o livro do topo pode se projetar em relação ao da base, de modo que
5.43. A barra uniforme AB possui peso de 75N . Determine a força no cabo quando a barra está na posição mostrada.
5.53. Determine o ângulo θ em que a ligação ABC se mantém em equilíbrio se o membro BD se mover 50m m para a direita. As molas estão originalmente descarregadas quando θ = 0 ° . Cada mola possui a rig
5.50. O vabo do guincho de um caminhão reboque está sujeito a uma força T = 6 k N quando o cabo está direcionado em θ = 60 ° . Determine as intensidades da força total de atrito do freio F para o conj
5.41. Determine as componentes horizontal e vertical da reação no pino A e a reação do colar liso B sobre a barra.