Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 36
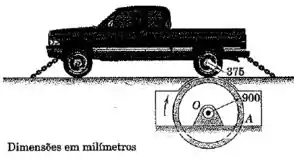
O dinamômetro automotivo é capaz de simular as condições rodoviárias para uma aceleração de para a caminhonete carregada, com uma massa total de . Calcule o momento de inércia necessário para o tambor do dinamômetro em relação ao seu centro supondo que o tambor gira livremente durante a fase de aceleração do teste.
Passo 1
Se a ideia é simular uma aceleração na roda traseira da caminhonete, então a força que o sistema deve imprimir sobre as rodas traseiras é:
E para essa aceleração linear de , a aceleração angular do tambor girando deve ser:
Passo 2
Então temos uma força de agindo a uma distância de do centro de massa do tambor, e gerando uma aceleração angular de .
Com essas informações fica fácil calcular o momento de inécia do tambor em relação a esse centro:
Resposta
O momento de inércia do tambor é .