Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas fundamentais - Ex. 7

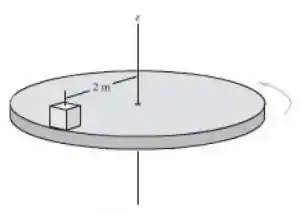
O bloco repousa a uma distância de 2 m do centro da plataforma. Se o coeficiente de atrito estático entre o bloco e a plataforma é μ s = 0,3 , determine a velocidade máxima que o bloco pode alcançar antes que comece a deslizar. Suponha que o movimento angular do disco está aumentando lentamente.

Passo 1

A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.

Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:

a n = v 2 ρ

Passo 2

Vamos começar por esboçar o diagrama de corpo livre do nosso problema. Desta forma, temos:

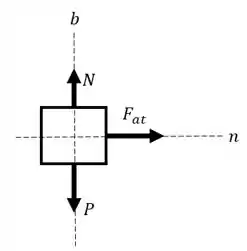
A força responsável por impedir o movimento do nosso bloco é a mesma responsável pela aceleração centrípeta, aquela que possibilita que ele mantenha uma trajetória curvilínea: a força de atrito! Portanto, basta relacionarmos a força de atrito com a força centrípeta.

Passo 3

Agora que já esboçamos o diagrama de corpo livre, para determinarmos a força de atrito, basta fazermos um somatório das forças na direção normal a trajetória. Desta forma, temos:

∑ F n = m ⋅ a n = m v 2 ρ

F a t = m v 2 ρ

N ⋅ μ s = m v 2 ρ

m g ⋅ μ s = m v 2 ρ

v = μ s ρ g = 0,3 ⋅ 2 ⋅ 9,81

v = 2,43   m / s

Resposta

v = 2,43   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3/59) As pequenas esferas são livres para se deslocar nasuperfície interna das câmaras esféricas rotativas rotativas mostradas em seção transversal com raio R = 200m m . Se as esferas atingem uma posi
3/51) Se o bloco de 2k g passa sobre o topo B da porção circular da trajetória com uma velocidade de 3,5m / s , calcule o módulo N B da força normal exercida pela trajetória sobre o bloco . Determine
3/55) O carro passa sobre o topo de uma curva num plano vertical em A com uma velocidade de 60k m / h e então passa pelo fundo de uma depressão em B . Os raios de curvatura da estrada em A e B são amb
3/57) O tubo vazado em torno do eixo horizontal que passa pelo ponto O e girano plano vertical com umavelocidade angular constante no sentido anti-horário θ ' = 3 r a d / s . Se uma partícula de 0,1k
3/63) Quando o esqueitista transpõe asuperfície mostrada , as velocidades do seu centro de massa em θ = 0 ° , 45 ° e 90 ° são 8,5m / s , 6m / s e 0 , respectivamente . Determine a força normal entre a