Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 45
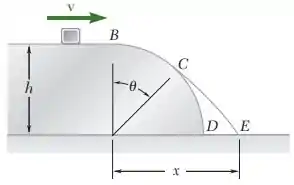
Um pequeno bloco desliza com uma velocidade sobre uma superfície horizontal. Sabendo que , determine a velocidade necessária para que ele deixe a superfície cilíndrica quando . Despreze o atrito e a resistência do ar.
Passo 1
Vamos lá! O interessante desta questão é que toda a informação necessária para resolver já foi desenvolvida na questão anterior, a 44! Assim, fica tudo muito mais fácil para a gente!
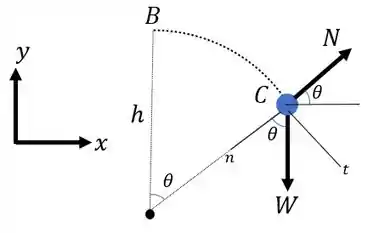
Se queremos que o bloco descole da superfície quando , então, é necessário que nesta posição a força normal seja nula. Relembrando da questão anterior, o diagrama do corpo livre do nosso problema é:
Passo 2
Agora que temos o diagrama de corpo livre, podemos fazer o somatório de forças na direção normal a trajetória. Cuidado para não esquecerem que o bloco possui uma aceleração centrípeta nesta direção!
Sendo assim, temos:
Como assumimos que a força normal é nula quando , temos:
Agora, vamos utilizar esta informação para descobrirmos a velocidade do bloco no ponto inicial!
Passo 3
Agora que descobrimos a velocidade do bloco no momento que ele descola da superfície, vamos descobrir a velocidade dele inicial. Para isto, vamos determinar as relações de energia cinética e trabalho, para podermos utilizar o princípio de trabalho e energia. Portanto,
Portanto, pelo princípio de trabalho e energia, temos:
E assim finalizamos a nossa questão!