Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 9

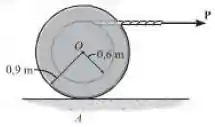
A bobina tem massa de 75   k g e raio de giração k O = 0,675   m . Se uma corda é enrolada em torno de seu miolo interno e sua extremidade é puxada com uma força horizontal P = 200   N , determine a velocidade angular da bobina após o centro O ter se movido 3   m para a direita. A bobina parte do repouso e não desliza em A enquanto rola. Despreze a massa da corda.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Como a bobina não desliza em A enquanto rola, temos que o ponto A é o nosso centro instantâneo de velocidade nula.

v O = ω r O / I C

v O = ω ( 0,9 )

Analisando geometricamente, temos que:

s P 0,9 + 0,6 = 3 0,9

s P = 5   m

Vejamos o diagrama de corpo livre:

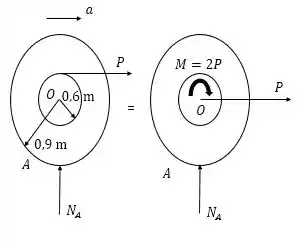
Passo 2

Podemos aplicar o princípio do trabalho e energia analisando o momento incial e final do sistema.

T 1 + ∑ U 1 → 2 = T 2

Temos que:

T 1 = 1 2 m v 1 2 + 1 2 I O ω 1 2

Como o momento inicial é o repouso, temos que:

T 1 = 0

Para o momento final, temos:

T 2 = 1 2 m v 2 2 + 1 2 I O ω 2 2

Sabendo que ω 2 = v 2 / r e I O = m O k O 2 :

T 2 = 1 2 75 0,9 ω 2 + 1 2 75 0,675 2 ω 2

T 2 = 47,46 ω 2

Passo 3

A parcela do trabalho ∑ U 1 → 2 , será:

∑ U 1 → 2 = P s P

∑ U 1 → 2 = 200 5

∑ U 1 → 2 = 1000   J

Agora é só aplicar:

T 1 + ∑ U 1 → 2 = T 2

0 + 1000   = 47,46 ω 2

ω = 4,6   r a d / s

Resposta

ω = 4,6   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra fina uniforme de 50 kg está em repouso na posição mostrada, quando P= 600N é aplicada. Determine a velocidade angular da barra quando ela atinge a posição vertical.
A roda de 20 kg tem um rio de giração em relação a se centro O, ko = 300 mm. Quando é submetida a um momento de binário M=50 N.m, ela rola sem deslizar. Determine a velocidade angular da roda após seu
Se a barra fina uniforme de 30 kg parte do repouso na posição mostrada, determine a velocidade angular após haver completado quatro revoluções. As forças permanecem perpendiculares à barra.
Uma polia dupla com massa de 25kg e um raio de giração em relação ao seu centro ko=0,24m, consiste em duas peças fixadas uma na outra. Ela gira no seu sentido horário a 20 rad/s, determinar a energia
O carretel de cabo que está em repouso, tem massa de 200Kg e um raio de giração Kg=325mm, quando uma força P=400N é aplicada no cabo conforme mostra a figura. Considerando que ele está sobre dois oequ