Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 59

A bobina uniforme está apoiada em dois roletes em A e B. Determine a força constante P que tem de ser aplicada ao cabo a fim de desenrolar 8 m de cabo em 4 s partindo do repouso. Também calcule as forças normais na bobina em A e B durante esse tempo. A bobina tem uma massa de 60 kg e um raio de giração em relação a O de k O = 0,65 m. Para o cálculo, despreze a massa do cabo e a massa dos roletes em A e B.

Passo 1

Inicialmente, vamos calcular a aceleração linear com que o cabo é desenrolado a partir da equação do deslocamento linear:

+ ↓   s = s 0 + v 0 t + 1 2 a c t 2

8 = 0 + 0 + 1 2 a c 4 2

a c = 1   m / s 2

Com isso, podemos encontrar a aceleração angular α através da seguinte equação:

α = a c r = 1 0,8 → α = 1,25   r a d / s 2

Passo 2

Agora, antes de calcular o somatório de momentos em torno do ponto O, devemos encontrar o valor do momento de inércia da bobina:

I O = m k O 2 = 60 0,65 2 → I O = 25,35   k g . m 2

Agora, calculando o somatório de momentos em torno do ponto O ilustrado na figura a seguir:

↻ + ∑ M O = ∑ I O α

P 0,8 = 25,35 1,25 → P = 39,6   N

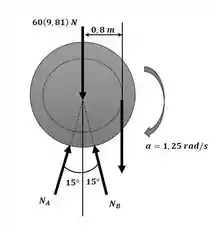
Passo 3

Agora iremos aplicar aplicar o somatório de forças na direção x e na direção y:

+ → ∑ F x = m a x

N A s e n 15 ° - N B s e n 15 ° = 0

N A = N B

+ ↑ ∑ F y = m a y

N A c o s 15 ° + N B c o s 15 ° - 39,6 - 588,6 = 0

N B c o s 15 ° + N B c o s 15 ° - 39,6 - 588,6 = 0

N A = N B = 325   N

Resposta

P = 39,6   N

N A = 325   N

N B = 325   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

97. Os dois discos idênticos estão girando livremente sobre o eixo, com velocidades angulares iguais em módulo e opostas em sentido como apresentado. O eixo por sua vez, é forçado a girar em torno do
105. A caixa retangular de paredes finas com extremidades abertas, de seção transversal quadrada, está girando no espaço em torno de seu eixo longitudinal central como mostrado. Se o eixo sofre uma li
103. O rotor de 210k g do motor de um avião turbojato tem um raio de giração de 220m m e gira no sentido anti-horário a 18000r p m quando visto de frente. Se o avião está viajando a 1200k m / h e come
100. O ventilador para uma aplicação especial é montado conforme mostrado. O rotor do motor, o eixo e as pás têm uma massa combinada de 2,2k g com raio de giração de 60m m . A posição axial b do bloco
104. Um pequeno compressor de ar para a cabine de um avião é composto pela turbina A de 3,50k g , que aciona o soprador B de 2,40k g a uma velocidade de 20000r p m . O eixo do conjunto está montado tr