Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 94
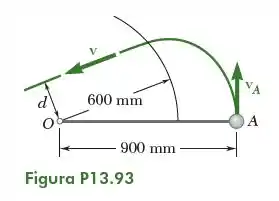
Para a bola do Problema 13.93, determine (a) o menor valor admissível da velocidade inicial para que a corda permaneça esticada todo tempo, (b) a velocidade máxima correspondente alcançada pela bola.
Passo 1
Olá, pessoal! Ânimo! Já, já vocês vão entender tudinho desse problema!
O problema pede que determinemos o menor valor admissível da velocidade inicial para que a corda fique sempre esticada, e a velocidade máxima que a bola alcança. Vamos iniciar essa resolução fazendo um esboço na situação enunciada.
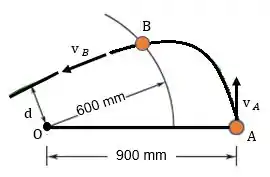
A bola é posta no ponto , a de , o que faz com que a corda seja esticada. Marcamos ali o ponto . Após ser solta, dali em diante, observe que a corda vai se afrouxando.
O enunciado do Problema 13.93 nos fornece os seguintes dados:
Passo 2
Posição A:
Vamos encontrar a deflexão da corda, , após a bola ser colocada no ponto A.
Em posse de , e sabendo que , vamos então encontrar a energia potencial .
Calculando a energia cinética , obtemos:
Passo 3
Posição B:
Passando desse ponto, a corda se torna frouxa, o alongamento é zero. Portanto,
E, calculando a energia cinética ,
Passo 4
Agora podemos aplicar a equação da conservação da energia:
Quando uma partícula se desloca sob a ação de forças conservativas, a soma da energia cinética e da energia potencial da partícula permanece constante. Assim, Eq. (13.24):
Substituindo, temos:
Passo 5
A alternativa a) pede a menor velocidade inicial para que a corda permaneça esticada o tempo todo, então, tendo isso em vista:
Agora, aplicando a equação conservação do momento angular:
Substituindo na equação encontrada no Passo 4, temos:
Passo 6
Em posse de , encontramos , que é a velocidade máxima correspondente alcançada pela bola: