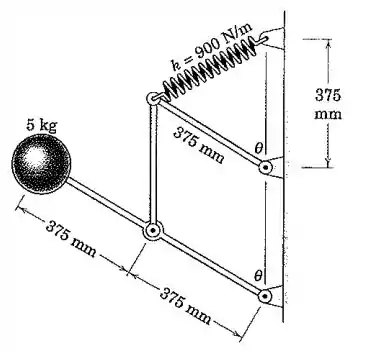
O mecanismo mostrado se situa no plano vertical e é liberado a partir do repouso na posição em que . Nesta posição a mola não está esticada. Calcule a velocidade da esfera de quando . A massa das conexões é pequena e pode ser desprezada.

Repare que na posição inicial, o triângulo cujo um dos lados é composto pela mola tem dois lados iguais de e um ângulo de entre eles. Isso significa que este é um triângulo equilátero, e portanto, o comprimento natural da mola é , já que ela não está esticada nessa posição.

Na posição final, quando , esse mesmo triângulo se transformará num triângulo retângulo, com catetos medindo . Então a deformação da mola pode ser encontrada assim:

Outra medida que podemos encontrar usando a geometria da figura é a altura inicial da esfera, considerando a altura zero como o suporte mais baixo da parede: