Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 155

A haste leve é articulada em O e carrega as partículas de 2 e 4   k g . Se a haste é liberada a partir do repouso em θ = 60 ° e oscila no plano vertical, calcule

(a) a velocidade v da partícula de 2   k g imediatamente antes que esta atinja a mola na posição tracejada e

(b) a compressão máxima x da mola.

Assuma que x é pequeno de modo que a posição da haste quando a mola é comprimida é essencialmente horizontal.

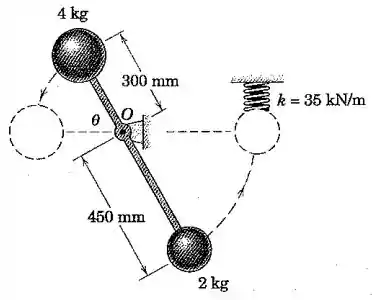
Passo 1

(a) A energia mecânica total do sistema é a soma das energias das duas partículas A e B , de 2 e 4   k g respectivamente. Vamos considerar a altura do centro O como a altura zero para calcular as energias inicial e final, beleza?

E 1 = T 1 + V 1 = 0 + m A g h A + m B g h B

E 1 = 2 9,81 - 0,450   s e n   60 ° + 4 9,81 0,300   s e n   60 °

E 1 = 2,549   J

E 2 = T 2 + V 2 = m A v A 2 2 + m B v B 2 2 + 0

E 2 = 2 v A 2 2 + 4 v B 2 2

E 2 = v A 2 + 2 v B 2

Como a energia do sistema se conserva, temos:

E 1 = E 2

2,549 = v A 2 + 2 v B 2

Passo 2

Note que as duas partículas estão em rotação em torno do mesmo eixo, mas com raios diferentes. Nesse caso, a velocidade angular é a mesma para as duas, ou seja,

ω = v A R A = v B R B

v A 0,450 = v B 0,300

v B = 2 3 v A

Substituímos isso na equação obtida com a conservação de energia:

2,549 = v A 2 + 2 2 3 v A 2

2,549 = v A 2 + 8 9 v A 2

v A = 1,162   m / s

Passo 3

(b) Vamos considerar a energia inicial E 1 como já calculada antes. A energia final E 3 no momento em que a partícula comprime ao máximo a mola é:

E 3 = T 3 + V 3 = 0 + k x 2 2

E 3 = 35 10 3 x 2 2

Pela conservação da energia mecânica do sistema:

E 1 = E 3

2,549 = 35 10 3 x 2 2

x = 0,01207   m

x = 12,07   m m

Resposta

(a) v = 1,162   m / s

(b) x = 12,07   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 18.11 usando a equação de conservação de energia.
Resolva o Problema 18.42 supondo que a corrente tenha uma massa por unidade de comprimento de 0,8k g / m . Despreze, para o cálculo, a porção da corrente que está encaixada na engrenagem.
O sistema consiste de um disco A , de 10k g , uma barra fina B C , de 2k g , e um anel liso C , de 0,5k g . Se o sico rola sem deslizar, determine a velocidade do anel no instante em que a barra torna
A porta de garagem uniforme tem massa de 150k g e é guiada ao longo de trilhos lisos em suas extremidades. A elevação é feita usando-se as duas molas, cada uma das quais fixada ao apoio de ancoragem e
Resolva o Problema 18.32 usando a equação de conservação de energia.