Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 157

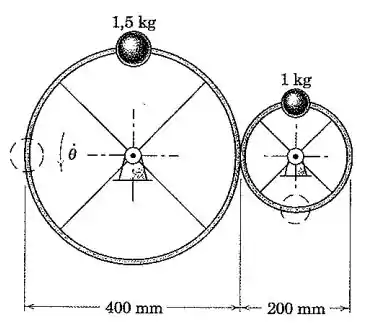
As duas rodas constituídas de aros e raios de massa desprezível giram em torno de seus respectivos centros e estão suficientemente pressionadas uma a outra de modo a evitar qualquer deslizamento. As massas excêntricas de 1,5   k g e 1   k g estão montadas sobre as bordas das rodas. Se as rodas recebem um leve desvio do repouso na posição de equilíbrio mostrada, calcule a velocidade angular θ ˙ da maior das duas rodas quando esta tiver girado através de um quarto de volta e colocado as massas excêntricas nas posições tracejadas mostradas. Note que a velocidade angular da roda pequena é duas vezes aquela da roda grande. Despreze qualquer atrito no mancal da roda.

Passo 1

Vamos chamar de A a massa de 1,5   k g e de B a massa de 1   k g . Então a variação da energia potencial gravitacional do sistema será:

Δ V = Δ V A + Δ V B = m A g Δ h A + m B g Δ h B

Considerando a altura do centro dos círculos como a altura zero, temos:

Δ V = 1,5 9,81 0 - 0,400 2 + 1 9,81 - 0,200 2 - 0,200 2

Δ V = - 4,905   J

Agora calculamos a variação da energia cinética do sistema, lembrando que, por causa da ligação entre as rodas, as massas têm a mesma velocidade linear:

Δ T = Δ T A + Δ T B = m A 2 v 2 - v 0 2 + m B 2 v 2 - v 0 2

Δ T = 1,5 2 v 2 + 1 2 v 2

Δ T = 1,25 v 2

Passo 2

Usando a conservação de energia mecânica, obtemos:

Δ T + Δ V = 0

1,25 v 2 - 4,905 = 0

v = 1,981   m / s

Porém, lembre-se que a velocidade angular se relaciona com a velocidade linear da seguinte forma:

θ ˙ = v r

Para a roda maior, temos r = 0,400 2   m , então:

θ ˙ = 1,981 0 , 200

θ ˙ = 9,90   r a d / s

Resposta

θ ˙ = 9,90   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

57. Determine a rigidez k da mola torcional em A, de modo que, se as barras são liberadas do repouso quando θ = 0 ° , a barra AB tenha uma velocidade angular de 0,5 rad/s na posição fechada, θ = 90 °
51. O pêndulo de 30kg tem seu centro de massa em G e raio de giração em relação ao ponto G de k G = 300m m . Se ele é solto do repouso quando θ = 0 ° , determine sua velocidade angular no instante θ =
50. O painel da porta retangular uniforme tem uma massa de 25 kg e é mantido em equilíbrio acima da horizontal, na posição θ = 60 ° pela barra BC. Determine a rigidez da mola torcional A, necessária p
54. Se a barra de 6 kg é liberada do repouso em θ = 30 ° , determine a velocidade angular da barra no instante θ = 0 ° . A mola a ela fixada tem rigidez k = 600 N/m, com um comprimento não deformado d
56. As barras AB e BC tem massa de 7,5 kg e 15 kg, respectivamente. O anel C, que desliza livremente ao longo da guia vertical lisa, tem massa de 2,5 kg. Se o sistema é liberado do repouso quando θ =