Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 111
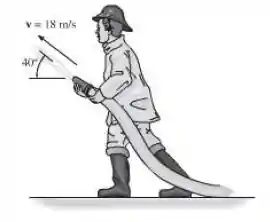
O bombeiro de está segurando uma mangueira que tem um diâmetro do bocal de e o diâmetro do corpo de . Se a velocidade da água na descarga é , determine as forças normal e de atrito resultantes agindo sobre os pés do homem no solo. Despreze o peso da mangueira e da água dentro dela.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Sabemos que:
Também podemos usar a relação:
Portanto:
Resposta
Exercícios de Livros Relacionados
Determine o módulo H 0 da quantidade de movimento angular da esfera de 2k g em torno do ponto O ( a ) usando a definição vetorial da quantidade de movimento angular e ( b ) usando uma abordagem escala
Uma partícula de massa m se desloca com atrito desprezível sobre uma superfície horizontal e está conectada a uma mola leve presa em O . Na posição A a partícula tem a velocidade v A = 4m / s . Determ
A partícula de massa m é suavemente empurrada a partir da posição de equilíbrio A e posteriormente desliza ao longo da trajetória circular lisa que se situa num plano vertical. Determine o módulo da s
A partícula de massa m é lançada a partir do ponto O com uma velocidade horizontal u no instante de tempo t = 0 . Determine sua quantidade de movimento angular H O em relação ao ponto O como uma funçã
Determine o módulo H O da quantidade de movimento angular em torno do ponto de lançamento O do projétil de massa m , que é lançado com velocidade v 0 no ângulo θ conforme indicado ( a ) no instante do