Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 74
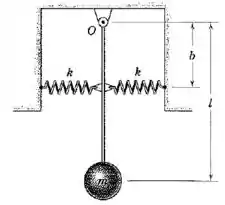
Desenvolva a equação diferencial para pequenas oscilações do pêndulo sob a ação das molas e determine o período . A posição de equilíbrio é vertical como indicada. A massa da haste é desprezível.
Passo 1
Vamos criar uma equação diferencial que dependa do ângulo da oscilação do pêndulo.
A melhor forma de fazer isso é escrevendo uma equação de momentos em torno do ponto :
Onde é a aceleração ângular associada ao ângulo , e é o momento de inércia do pêndulo simples:
Vamos fazer um diagrama de um instante em que o pêndulo está deslocado por um pequeno ângulo :
Nesse caso estamos considerando que as molas permanecem na horizontal, o que é uma aproximação razoável para ângulos pequenos.
Passo 2
Para escrever os módulos das forças e , precisamos encontrar uma expressão para a distorção das molas:
E as duas forças sempre apontam na mesma direção, e tem o mesmo módulo, já que a distorção das duas molas é sempre igual.
Olhando para o desenho do enunciado, vemos que as molas estão presas no cabo a uma distância do ponto , então:
Agora podemos completar nossa equação de momentos:
E o sinal negativo aparece porque esses momentos agem no sentido que diminui .
Para ângulos pequenos, podemos substituir e , então:
Dividindo tudo por , ficamos com a seguinte equação:
Passo 3
Para encontrar o período a partir dessa equação, temos que nos lembrar da forma geral de uma equação de oscilador harmônico:
Onde é a frequência angular. Comparando com a nossa equação do passo anterior, vemos que:
E a relação entre e o período é a seguinte:
Então:
Resposta
A equação é e o período é .