Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 81

O disco tem uma massa de 20 kg e está originalmente girando na extremidade da escora com uma velocidade angular ω = 60 rad/s. Se ele é, então, colocado contra a parede, onde o coeficiente de atrito cinético é μ k = 0,3, determine o tempo necessário para o movimento parar. Qual é a força na escora BC durante esse tempo?

Passo 1

Iremos considerar a aceleração da gravidade g = 9,81   m / s 2

Iremos começar aplicando as equações do movimento para o sistema com o auxílio do esquema a seguir:

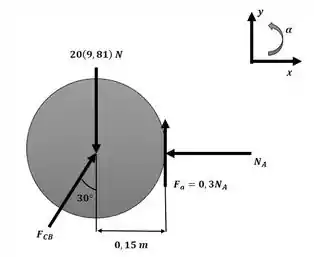
Na direção x:

+ → ∑ F x = ∑ m a G x

F C B s e n 30 ° - N A = 0

Essa será nossa equação 1.

Na direção y:

+ ↑ ∑ F y = ∑ m a G y

F C B c o s 30 ° - 20 9,81 + 0,3 N A = 0

Essa será nossa equação 2.

Equação do momento:

↺ + ∑ M B = ∑ I B α

0,3 N A 0,15 = 1 2 20 0,15 2 α

Essa será nossa equação 3.

Passo 2

Agora, resolveremos o sistema de equações encontrado no passo anterior. Começaremos isolando N A da equação 1 e substituindo na 2:

F C B c o s 30 ° - 20 9,81 + 0,3 N A = 0

F C B c o s 30 ° - 20 9,81 + 0,3 ( F C B s e n 30 ° ) = 0

F C B = 193,1   N

Agora podemos encontrar o valor de N A através da equação 1:

F C B s e n 30 ° - N A = 0

( 193,1 ) s e n 30 ° - N A = 0

N A = 96,55   N

E, finalmente, substituindo esse valor na equação 3:

0,3 N A 0,15 = 1 2 20 0,15 2 α

0,3 ( 96,55 ) 0,15 = 1 2 20 0,15 2 α

α = 19,31   r a d / s 2

Passo 3

Com a aceleração, podemos encontrar o tempo necessário de parada:

ω = ω 0 + α t

0 = 60 + ( - 19,31 ) t

t = 3,11   s

Resposta

t = 3,11   s

F C B = 193,1   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada uma das hastes esbeltas de comprimento l e massa m está soldada ao disco circular que gira em torno do eixo vertical z com uma velocidade angular ω . Cada haste faz um ângulo β com a vertical e e
O conjunto que consiste na esfera maciça de massa m e na barra uniforme de comprimento 2c e massa igual m, gira em torno do eixo vertical z com uma velocidade angular ω . A barra de comprimento 2c tem
Em um teste dos painéis solares para uma nava espacial, o modelo apresentado está girando em torno do eixo vertical na velocidade angular ω . Se a massa por unidade de área do painel é ρ , escreva a e
Utilize os resultados do Prob. 7/55 e determine a quantidade de movimento angular H g dobrada daquele problema em relação ao seu centro de massa G utilizando os eixos de referência fornecidos.
O disco circular uniforme do Prob. 7/48, com três componentes de velocidade angular, é mostrado novamente aqui. Determine a energia cinética T e a quantiadde de movimento angular H o , para o instante