Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 49
A motoesqui tem uma massa de 125 kg, centrada em , enquanto o motorista tem uma massa de 75 kg, centrada em . Se a aceleração é a = 6 m/s², determine a altura máxima h de do motorista, tal que o esqui frontal da motoesqui não saia do solo. Também, qual é a força de tração (horizontal) e a reação normal sob as esteiras traseiras em A?
Passo 1
Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².
Uma vez que o enunciado pede a altura máxima desde que o esqui frontal não saia do solo, analisaremos o caso limite, onde:
E aplicaremos o somatório de momentos em torno do ponto A ilustrado na figura a seguir, para descobrir a altura máxima h:
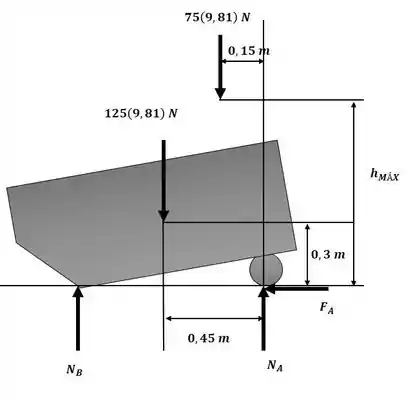
Passo 2
Agora iremos aplicar o somatório de forças na direção x para descobrir a força de tração no ponto A:
Passo 3
Por fim, para descobrirmos a reação normal no ponto A, iremos aplicar o somatório de forças na direção y: