Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 53
A caixa uniforme de 50 kg repousa sobre a plataforma para a qual o coeficiente de atrito estático é . Se no instante os membros-apoio têm uma velocidade angular rad/s e aceleração angular rad/s², determine a força de atrito sobre a caixa.
Passo 1
Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².
Primeiramente devemos decompor a velocidade, e consequente aceleração angular fornecida, em suas componentes normal e tangencial da seguinte forma:
Agora podemos analisar a equivalência dos sistemas conforme a ilustração a seguir:
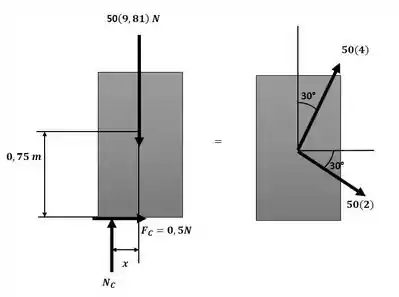
Passo 2
Agora iremos aplicar o somatório de forças nos eixos x e y para descobrir os valores de e :
Devemos verificar a condição da força de atrito:
Podemos verificar que , logo, a condição em análise é válida.
Passo 3
Agora, iremos aplicar o somatório de momentos em torno do centro de massa da caixa para descobrir se o ponto de apoio se encontra “na caixa”:
Essa distância deve ser menor que 0,25m, uma vez que a caixa possui 0,5 m de largura e a distância x é avaliada a partir do centro da caixa, sendo assim, o ponto de apoio está localizado a 0,228 m do centro da caixa, logo, a força de atrito encontrada no passo 2 é válida.