Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 51

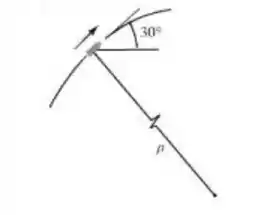
No instante mostrado, o raio de curvatura da trajetória vertical do projétil de 50   k g é ρ = 200   m . Determine a velocidade do projétil neste instante.

Passo 1

Temos que tomar bastante cuidado com este problema, pois a figura não ajuda o tanto que ela deveria. O que acontece é que o projétil percorre uma trajetória circular no plano y z . Portanto, ele está sujeito ao seu peso. É esta força que será responsável por conferir uma componente tangencial e uma componente normal a aceleração. Portanto, precisamos começar esboçando o diagrama de corpo livre para entender a configuração dessas forças inicialmente. Só depois que poderemos partir para o cálculo da cinemática!

Passo 2

Conforme dito no Passo 1, começaremos esboçando o diagrama de corpo livre do problema. Portanto,

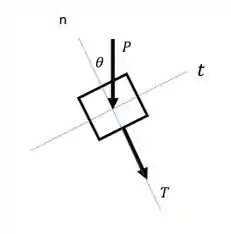
A força peso possui uma inclinação de θ = 30 ° em relação a direção normal. Portanto,

↖ ∑ F n = m ⋅ a n

- P cos ⁡ θ = m ⋅ a n

- 50 ⋅ 9,81 ⋅ cos ⁡ 30 = 50 ⋅ a n

a n = 8,496   m / s 2

Passo 3

Agora que descobrimos o valor da componente normal da aceleração, basta aplicarmos na sua equação da cinemática para descobrirmos a sua velocidade. Portanto,

a n = v 2 ρ

8,496 = v 2 200

v = 41,2   m / s

Resposta

v = 41,2   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o foguete deve pousar na superfície do planeta, determine a velocidade escalar de voo livre necessária que ele dever ter em A ' de maneira que ele atinja o planeta em B . Quanto tempo leva para o f
Se o foguete deve pousar na superfície do planeta, determine a velocidade escalar de voo livre que ele deve ter em A ' de maneira que o pouso ocorra em B . Quanto tempo o foguete leva para pousar, ind
Resolva o Problema 13.114 se o braço tem aceleração angular de θ ¨ = 2r a d / s 2 quando θ ˙ = 3r a d / s a θ = 30 ° .
Determine a velocidade escalar constante do satélite S de maneira que ele circule a Terra com uma órbita de raio r = 15M m . Dica: utilize a Equação 13.1.
O satélite está em uma órbita elíptica tendo uma excentricidade de e = 0,15 . Se a sua velocidade no perigeu é v P = 15M m / h , determine a sua velocidade no apogeu A e o período do satélite.