Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 95
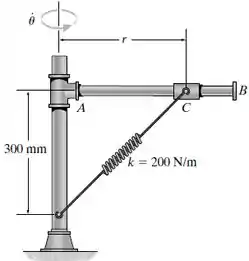
Um mecanismo está girando em torno do eixo vertical com velocidade angular constante de . Se a barra é lisa, determine a posição constante do anel de 3 kg. A mola tem um comprimento não deformado de 400 mm. Despreze a massa da barra e a dimensão do anel.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do anel :
Velocidade angular constante:
Posição fixa do anel:
Comprimento não deformado da mola:
Constante elástica da mola:
A questão pede para determinar a posição do anel com a condição de que esta seja constante.
Portanto, temos que , e são constantes, ou seja, não variam no tempo.
Desenhamos o diagrama de corpo livre do anel .
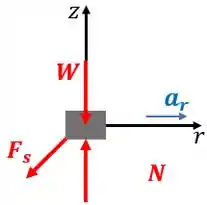
Onde é a força peso, , é a força normal e é a força elástica.
Passo 2
Primeiramente, vamos encontrar as derivadas temporais.
Como , e são constantes, obtemos os seguintes valores:
Passo 3
Sabemos que as componentes da aceleração do anel nas coordenadas , e são dadas por
Logo,
Passo 4
Sabemos que a força elástica é dada pela seguinte fórmula:
Precisamos encontrar o comprimento final da mola e o ângulo com que esta força está sendo aplicado no anel. Analisando a situação geometricamente, temos
Sabemos que
m
Portanto,
Agora vamos encontrar o valor de :
Passo 5
Agora aplicaremos as Equações do Movimento.
Analisando no eixo , temos que