Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 11

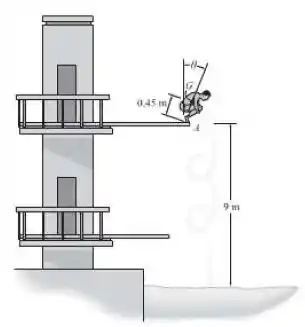
Um homem com massa de 75   k g está agachado na extremidade do trampolim, como mostra a figura. Nessa posição, o raio de giração em relação a seu centro de gravidade é k G = 0,36   m . Enquanto mantém sua posição em θ = 0 ° , ele gira em torno da ponta dos pés em A , até que perca contato com a plataforma, quando θ = 90 ° . Se ele permanece rígido, determine de forma aproximada quantas revoluções ele completará antes de atingir a água, após uma queda de 9   m .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Podemos aplicar o princípio do trabalho e energia analisando o momento incial e final do sistema.

T 1 + ∑ U 1 → 2 = T 2

Temos que:

T 1 = 1 2 m v 1 2 + 1 2 I O ω 1 2

Como o momento inicial é o repouso, temos que:

T 1 = 0

Para o momento final, temos:

T 2 = 1 2 m v 2 2 + 1 2 I O ω 2 2

Sabendo que ω 2 = v 2 / r e I O = m O k O 2 :

T 2 = 1 2 75 0,45 ω 2 + 1 2 75 0,36 2 ω 2

T 2 = 12,45 ω 2

Passo 2

A parcela do trabalho ∑ U 1 → 2 , será:

∑ U 1 → 2 = m g h

∑ U 1 → 2 = 75 9,81 0,45

∑ U 1 → 2 = 331,1   J

Agora é só aplicar:

T 1 + ∑ U 1 → 2 = T 2

0 + 331,1   = 12,45 ω 2

ω = 5,16   r a d / s

Logo:

v G = 0,45 ( 5,16 )

v G = 2,32   m / s

Passo 3

Agora que temos a velocidade do centro de massa, podemos encontrar o tempo de queda a partir da equação da posição do movimento acelerado.

Temos que:

s = s 0 + v 0 t + 1 2 a t 2

9 = 0 + 2,32 t + 1 2 9,81 t 2

4,905 t 2 + 2,32 t - 9 = 0

t = 1,147   s

Podemos associar o tempo com a posição θ do nadador. Logo:

θ = θ 0 + ω 0 t + 1 2 α t 2

θ = 0 + 5,16 1,147 + 0

θ = 5,92   r a d

Sabendo que 2 π equivale a uma volta, temos que:

θ = 0,942   r e v

Resposta

θ = 0,942   r e v

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Bolas de gude tendo massa de 5 g caem do repouso em A através do tubo de vidro e se acumulam na vasilha em C . Determine a posição R da vasilha no fim do tubo e a velocidade na qual as bolas de gude c
Se a pista deve ser projetada de maneira que os passageiros do carro da montanha-russa não sintam uma força normal igual a zero ou mais do que 4 vezes o seu peso, determine as altura limitantes h A e
A roda de 80 kg tem um raio de giração em relação a seu centro de massa O, ko = 400 mm. Determine a velocidade angular após haver completado 20 revoluções, partindo do repouso.
A roda de 50 kg é submetida a uma forca d 50 N. Se a roda parte do repouso e rola sem deslizar, determine sua velocidade angular depois de haver completado 10 revoluções. O raio de giração da roda em
A barra fina uniforme de 25 kg é submetida a um momento de binário M = 150 N.m. Se a barra está em repouso quando θ = 0 ° , determine a velocidade angular quando θ = 90 ° .