Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 75

Determine a aceleração angular do trampolim de 25 kg e as componentes verticais e horizontais da reação no pino A no instante em que o homem realiza o salto. Suponha que a tábua do trampolim seja uniforme e rígida e que, no instante em que ele salta, a mola está comprimida uma quantidade máxima de 200 mm, = 0 e a tábua está na horizontal. Considere k = 7kN/m.

Passo 1

Nesse exercício, iremos adotar a aceleração da gravidade como .

Usaremos o seguinte diagrama de corpo livre para analisar o problema:

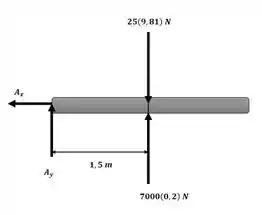
Iremos primeiramente calcular o momento de inércia do trampolim:

Passo 2

Agora iremos decompor a aceleração angular em suas componentes normal e tangencial:

Passo 3

Agora, aplicando o somatório de momento em torno do ponto A:

E agora, aplicando o somatório de forças.

Na direção normal:

Na direção tangencial:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

145. Calcule o momento fletor M no eixo O para o conjunto em rotação do Prob 7 / 144 , quando parte do repouso com uma aceleração angular inicial de 200r a d / s 2 .

143. Cada uma das duas barras dobradas em ângulo reto possui uma massa de 1,2k g e é paralela ao plano horizontal x - y . As barras estão soldadas à haste vertical, que gira em torno do eixo z com uma

146. Desenvolva a Eq. 7 / 24 , relacionando as forças às acelerações para um elemento diferencial do anel fino de massa m . O anel possui uma velocidade angular constante p em torno do eixo z e recebe

142. O desbalanceamento dinâmico de um determinado virabrequim é aproximado pela modelo físico apresentado, onde o eixo sustenta três esferas pequenas de 0,6k g fixadas por hastes de massa desprezível

144. Cada uma das placas com o formato de um quadrante de círculo possui uma massa de 2k g e está presa ao eixo vertical montado no mancal fixo em O . Calcule o módulo M do momento fletor no eico em O