Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 100

O duto de concreto circular rola com uma velocidade angular de ω = 0,5   r a d / s quando o homem está na posição mostrada. Nesse instante, o centro de gravidade do duto e do homem está localizado no ponto G, e o raio de giração em relação a G é k G = 1,05   m . Determine a aceleração angular do duto. A massa combinada do duto e do homem é de 250 kg. Suponha que o duto rola sem deslizar, e o homem não se desloca dentro dele.

Passo 1

Começaremos o exercício calculando o momento de inércia do duto em relação ao seu centro de massa:

I G = m k G 2 = 250 1,05 2 → I G = 275,625   k g . m 2

Podemos aplicar o somatório de momentos com relação ao ponto A ilustrado na imagem a seguir:

↺ +   ∑ M A = ∑ M k A

- 250 9,81 0,15 = - 250 a G x 1,2 - 250 a G y 0,15 - 275,625 α

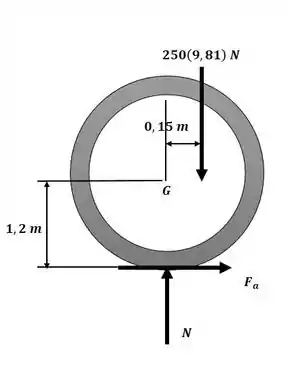
Essa será nossa equação 1.

Passo 2

Uma vez que o duto rola sem deslizar, podemos escrever:

a 0 = α r = α ( 1,2 )

Agora podemos aplicar a equação da aceleração vista no capítulo 16 com o auxílio da imagem a seguir:

a G = a O + α × r G / O - ω 2 r G / A

a G x i - a G y j = 1,2 α i + - α k × 0,15 i - 0,5 2 ( 0,15 i )

a G x i - a G y j = 1,2 α - 0,0375 i - 0,15 α j

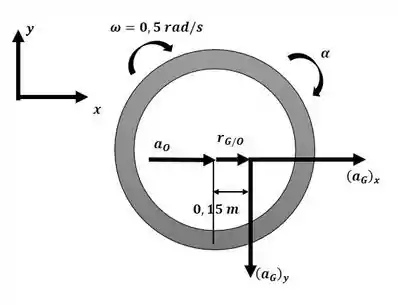
Igualando as componentes:

a G x = 1,2 α - 0,0375

a G y = 0,15 α

Essas são nossas equações 2 e 3.

Passo 3

Agora iremos substituir as equações 2 e 3 na equação 1:

- 250 9,81 0,15 = - 250 a G x 1,2 - 250 a G y 0,15 - 275,625 α

- 250 9,81 0,15 = - 250 ( 1,2 α - 0,0375 ) 1,2 - 250 ( 0,15 α ) 0,15 - 275,625 α

α = 0,591   r a d / s 2

Resposta

α = 0,591   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o apoio em B é subitamente removido, determine as componentes vertical e horizontal iniciais da reação que o pino A exerce sobre a barra ACB. Os segmentos AC e CB têm, cada um, uma massa de 5 kg.
O pêndulo de 100 kg tem um centro de massa em G e um raio de giração em relação a G de k G = 250 mm. Determine as componentes verticais e horizontais da reação do pino A e da reação normal do rolete B
O pêndulo de 100 kg tem um centro de massa em G e um raio de giração em relação a G de k G = 250 mm. Determine as componentes verticais e horizontais da reação do pino A e da reação normal do rolete B
A barra fina de comprimento L e massa m é solta do repouso quando θ = 0°. Determine como uma função de θ as forças normal e de atrito que são exercidas pelo degrau sobre a barra em A na medida em que
As rodas A e B têm uma massa de 75 kg e 50 kg, respectivamente. Inicialmentem a roda A gira no sentido horário com uma velocidade angular constante de ω = 100 rad/s e a roda B está em repouso. Se A é