Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 132

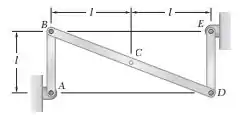
No instante mostrado na figura, a barra AB tem uma aceleração angular nula e uma velocidade angular constante de 8 rad/s no sentido horário. Sabendo que l = 0,3 m, determine a aceleração do ponto médio C do membro BD.

Passo 1

Vamos lá responder mais essa. As velocidades dos pontos B e D tem sentido positivo, e ω A B = 8 rad/s, no sentido horário. Assim a velocidade do ponto B pode ser escrita como:

v B = A B ω A B = 0,3 ⋅ 8 = 2,4   m / s

Como o centro instantâneo da barra BD está em um ponto localizado no infinito, ω B D = 0 e v D = v B = 2,4   m / s . Para a barra DE, temos:

ω D E = v D D E = 2,4 0,3 = 8   r a d / s     ( s e n t i d o   a n t i - h o r á r i o )

Passo 2

Como a barra AB tem velocidade angular constante, temos que α A B = 0 . Assim, avaliando a aceleração de D em relação a B temos:

a → D = a → B + a → D / B

a B = α A B k → × A B j → - ω A B 2 A B j → = - 0,3 ⋅ 8 2 j → =   - 19,2 j →

a → D / B = α B D k → × 2 l i → + α B D k → × - l j → - ω B D 2 2 l i → - ω B D 2 - l j → = 0,6 α B D j → + 0,3 α B D i →

a → D = α D E k → × - l j → - ω D E 2 - l j → = 0,3 α D E i → + 19,2 j →

0,3 α D E i → + 19,2 j → =   - 19,2 j → +   0,6 α B D j → + 0,3 α B D i →

Passo 3

Resolvendo cada componente:

19,2   =   - 19,2 + 0,6 α B D → α B D = 64   r a d / s 2

Analisando a aceleração do ponto C em relação a B:

a → C = a → B + a → C / B

a → C / B = 1 2 a → D / B = 0,15 α B D i → + 0,3 α B D j → = 9,6 i → + 19,2 j →  

a → C = - 19,2 j → + 9,6 i → + 19,2 j → = 9,6 i →

a C = 9,6   m / s 2

Resposta

9,6 m/s²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bola C se desloca ao longo da ranhura de A para B com uma velocidade de 0,9 m/s e aceleração de 0,45 m/s2, ambas medidas em relação à placa circular. Nesse mesmo instante, a placa gira com a velocid
Determine a velocidade angular e acelaração angular da placa CD do mecanismo triturador de pedras no instante em que AB está na horizontal. Neste instante, θ = 30 ° e ϕ = 90 ° . O membro de acionament
Um homem está parado na plataforma em O e corre para fora na dreção da beira da plataforma de tal maneira que, quando eles está em A, y=1,5m, seu centro de massa tem uma velocidade de 0,6 m/s e uma ac
O raio do pino B fixo à manivela AB desliza livremente ao longo da ranhura no membro CDE. Se AB gira com o movimento mostrado, determine a velocidade angular de CDE no instante mostrado.
A lança telescópica do guindaste gira com a velocidade angular e a aceleração angular mostradas. No mesmo instante, a lança está se estendendo com uma velocidade constante de 0,15 m/s, medida em relaç