Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 6

Calcule o centroide da área a seguir:

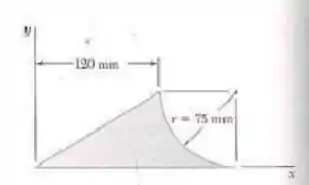
Passo 1

Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine o centroide da área dada. Para isso, vamos dividir a área em figuras conhecidas.

Logo, o centroide será o produto do centroide do quadrado pela sua área mais o centroide do triângulo pela sua área, menos o centroide do quarto de círculo pela sua área, isso tudo dividido pelas áreas do retângulo mais a do quadrado menos a do quarto de círculo. Logo:

A xx overset(-)(x)_t r i â n g u l o = 80 xx 75 xx (120)/(2) = 360000

A xx overset(-)(y)_t r i â n g u l o = 25 xx 75 xx (120)/(2) = 112500

Já o do quadrado será:

A xx overset(-)(x)_q u a d r a d o = 157,5 xx 75 ² = 885937,5

A xx overset(-)(y)_q u a d r a d o = 37,5 xx 75 ² = 210937,5

O do quarto de círculo será:

A xx overset(-)(x)_c i r c = (195 - 4 xx (75)/(3 pi)) xx (1)/(4) xx pi xx 75^2 = 720858,61

A xx overset(-)(y)_c i r c = (75 - 4 xx (75)/(3 pi)) xx (1)/(4) xx pi xx 75^2 = 190714,85

Portanto:

overset(-)(x) = (525078,89)/(5707,13) = 92,004 m m

overset(-)(y) = (132722,65)/(5707,13) = 23,25 m m

Resposta

overset(-)(x) = 92,004 m m

overset(-)(y) = 23,25 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume e a localização do centroide ( y - , z - ) do calço cônico homogêneo.
Localize o centro de massa y - do cone circular formado girando-se a área sombreada em torno de eixo y . A densidade em qualquer ponto no cone é definida por ρ = ρ 0 h y , onde ρ 0 é uma constante.
O corpo homogêneo mostrado é constituído a partir do corpo sólido do Prob. 5/211 e, a seguir, removendo um volume cilíndrico com um diâmetro pouco menor que R , como mostrado, deixando uma parede fina
A figura mostra um corpo semelhante ao do Prob. 5/211, mas agora o corpo é uma casca fina com aberturas na base e no topo. Determine a altura h - de seu centro de massa, acima da base do sólido homogê
A barra uniforme de massa m está curvada em um quarto de arco circular, no plano vertical, e bascula livremente em A . A barra é mantida em posição pelo arame horizontal de O até B . Determine o módul