Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 14

Calcule o centroide da área a seguir:

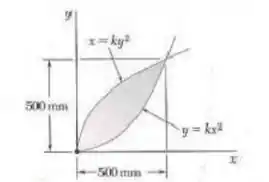
Passo 1

Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine o centroide da área dada. Para isso, vamos dividir a área em figuras conhecidas.

Logo, o centroide será o produto do centroide do quadrado pela sua área menos os produtos dos centroides das parábolas pelas suas áreas, divididos pela área do quadrado menos a área das parábolas. Logo:

A xx overset(-)(x)_q u a d r a d o = 250 xx 500^2 = 62500000

A xx overset(-)(y)_q u a d r a d o = 250 xx 500^2 = 62500000

O da parábola de segundo grau superior será:

A xx overset(-)(x)_p a r a b o l a s = 500 xx (500)/(3) xx ( 500 - 3 xx (50 0)/(4) ) = 10416666,67

A xx overset(-)(y)_p a r a b o l a s = 500 xx (500)/(3) xx (500 - 3 xx (500)/(10)) = 29166666,67

O da parábola de segundo grau inferior será:

A xx overset(-)(x)_p a r a b o l a s = 500 xx (500)/(3) xx ( 3 xx (500)/(4) ) = 31250000

A xx overset(-)(y)_p a r a b o l a s = 500 xx (500)/(3) xx (3 xx (500)/(10)) = 12500000

Portanto:

overset(-)(x) = (20833333,33)/(83333,33) = 250 m m

overset(-)(y) = (20833333,33)/(83333,33) = 250 m m

Este resultado também pode ser observado por simetria.

Resposta

overset(-)(x) = 250 m m

overset(-)(y) = 250 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área e o centroide ( overset(-)(x) , overset(-)(y) ) da área.
Determine a área e o centroide (overset(-)(x) , overset(-)(y)) da área.
Localize o centroide overset(-)(x) da área.
Localize o centroide ( overset(-)(x) , overset(-)(y) ) da área.
Determine a área e o centroide (overset(-)(x) , overset(-)(y)) da área.