Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 12

Localize o centroide overset(-)(x) da área.

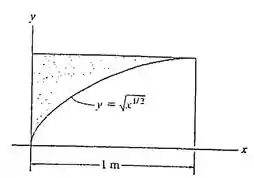
Passo 1

Primeira vamos encontrar a área do nosso elemento diferencial, que é a área em cinza na figura:

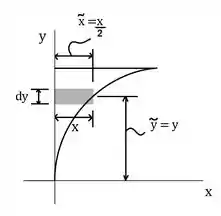
Essa área é dada por:

d A = x ⅆ y

Colocando nossa função em função de y temos x = y^4 , nosso d A fica:

d A = y^4 d y

Para o centroide do nosso elemento diferencial overset(-)(x) será:

overset(-)(x) = (x)/(2) = (y^8)/(2)

Passo 2

Vamos encontrar nossa área:

A = int_A ⅆ A

Descobrindo nosso limite de integração quando x = 1 m :

y (1) = 1^((1)/(4)) = 1

Logo, nossa área fica:

A = int_0^1 y^4 d y =

A = [(y^5)/(5)]_0^1

A = (1)/(5) m^2

Passo 3

E agora encontramos nosso centroide para overset(-)(x) :

overset(-)(x) = (int_A overset(-)(x) ⅆ A)/(int_A ⅆ A)

overset(-)(x) = (int_0^1 (y^8)/(2) (y^4 d y))/((1)/(5)) = (int_0^1 (1)/(2) x^(12) ⅆ x)/((1)/(5)) = (((1)/(2) * (x^(13))/(13)|_0^1)/((1)/(5)) = ((1)/(26))/((1)/(5)) = (5)/(26)

Resposta

overset(-)(x) = (5)/(26) m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centro de massa x - da barra reta se sua massa por unidade de comprimento for dada por m = m o 1 + x 2 L 2 .
Determine o centróide y - da area sombreada.
Determine o centróide ( x - , y - ) da area sombreada.
Localize o centroide y - do sólido homogêneo formado girando-se a área sombreada em torno do eixo y .
Localize o centroide z - do sólido homogêneo formado girando-se a área sombreada em torno do eixo z .