Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 52

No instante θ = 30 ° , a estrutura do guindaste e a lança A B giram com uma velocidade angular constante ω 1 = 1,5   r a d / s e ω 2 = 0,5   r a d / s , respectivamente. Determine a velocidade e a aceleração do ponto B nesse instante.

Passo 1

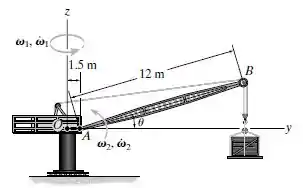
Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos às analises:

v A = ω 1 × r O A

v A = 1,5 k × 1,5 j = - 2,25 i   m / s

a A = ω ˙ 1 × r O A + ω 1 × ω 1 × r O A

a A = 0 + 1,5 k × 1,5 k × 1,5 j

a A = - 3,375 j   m / s 2

Temos que:

Ω x y z = 0,5 i

Ω ˙ x y z = 0

r B / A = 12 cos ⁡ 30 ° j + 12 sin ⁡ 30 ° k

r B / A = 10,4 j + 6 k

v B / A = r ˙ B / A = r ˙ B / A x y z + Ω x y z × r B / A

v B / A = 0 + 0,5 i × 10,4 j + 6 k

v B / A = - 3 j + 5,196 k

a B / A = r ¨ B / A = r ¨ B / A x y z + Ω x y z × r ˙ B / A + Ω ˙ x y z × r B / A + Ω x y z × r ˙ B / A

a B / A = 0 + 0 + 0 + 0,5 i × - 3 j + 5,196 k

a B / A = ( - 2,598 j - 1,5 k )

Como Ω = 1,5 k e Ω ˙ = 0 , temos:

v B = v A + Ω × r B / A + v B / A

v B = - 2,25 i + 1,5 k × 10,4 j + 6 k + - 3 j + 5,196 k

v B = ( - 17,8 i - 3 j + 5 , 2 k )   m / s

Temos também que:

a B = a A + Ω ˙ × r B / A + Ω × ( Ω × r B / A ) + 2 Ω × v B / A + a B / A

a B = - 3,375 j + 0 + 1,5 k × 1,5 k × 10,4 j + 6 k + 2 1,5 k × - 3 j + 5,196 k + ( - 2,598 j - 1,5 k )

a B = ( 9 i - 29,4 j - 1,5 k )   m / s 2

Resposta

v B = ( - 17,8 i - 3 j + 5,2 k )   m / s

a B = ( 9 i - 29,4 j - 1,5 k )   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O transporte aéreo B está voando com uma velocidade constante de 800 km/h em um arco horizontal com 15 km de raio. Quando B atinge a posição mostrada, a aeronave A, voando para sudoeste a uma velocida
Uma pista de boliche lisa é orientada na direção norte-sul como mostrado. Uma bola A é liberada com uma velocidade v ao longo da pista conforme indicado. Em função do efeito de Coriolis, a bola desvia
Para as condições do prob. 5/173 obtenha a expressão vetorial para a aceleração que a aeronave A aparenta ter para um observador interior de B e girando com a aeronave B, na qual os eixos x-y estão fi
Os carros A e B estão contornando as curvas com velocidades iguais 72 km/h. Determine a velocidade que A parece ter para um observador se deslocando e girando com o carro B para o instante representad
Um edifício alto está situado sobre o equador. O lado norte do edifício aloja um relógio de 12 horas comum cujo centro está a uma distância h acima do chão (que está aproximadamente ao nível do mar).