Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 92

O carrinho de montanha-russa, tendo massa m, é solto do repouso no ponto A . Se a pista precisa ser projetada de maneira que o carrinho não a deixe em B , determine a altura necessária h . Além disso, determine a velocidade do carrinho quando ele chega ao ponto C . Despreze o atrito.

Passo 1

Como é necessário que o carro da montanha-russa esteja prestes a sair do trilho em B, a força normal é zero N B = 0 . Conforme o DCL mostrado.

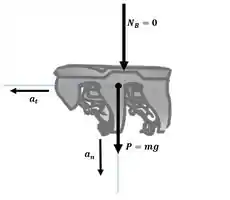
Fazendo os somatórios de forças

∑ F n = m a n

P = m g = m a n

Sendo,

a n = v B 2 ρ B =   v B 2 7,5

Então,

m 9,81 = m v B 2 7,5

v B 2 = 73,575   m 2 / s 2    

Passo 2

Para calcular a altura h , é necessária determinar as energias potenciais gravitacionais paras os pontos A , B   e   C .

E g A = m g h A = 9,81 m h

E g B = m g h B = m 9,81 20 = 196,2 m

E g C = m g h c = m 9,81 0 = 0

Passo 3

Aplicando a conservação de energia, usando o resultado de v B 2 considerando o movimento do carro de A para B.

E C A + E g A =   E C B + E g B

1 2 m v A 2 + 9,81 m h =   1 2 m v B 2 + 196,2 m

0 + 9,81 m h =   1 2 m 73,575 + 196,2 m

h = 23,75   m

Aplicando a conservação de energia, usando o resultado de v B 2 considerando o movimento do carro de B para C.

E C B + E g B =   E C C + E g C

1 2 m v B 2 + 196,2 m =   1 2 m v C 2 + 0

1 2 m ( 73,575 ) + 196,2 m =   1 2 m v C 2 + 0

v c = 21,6   m / s

Resposta

A altura necessária h   para que o carrinho não caia em B é de 23,75   m .

E a velocidade que o carrinho passa em C é 21,6   m / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um satélite é posto em uma órbita elíptica em torno da Terra. Sabendo-se que a razão v A / v P entre as velocidades no apogeu A e no perigeu P é igual à razão r P / r A , entre as distâncias de P e A
Enquanto descreve uma órbita circular a 300 km acima da Terra, um veículo espacial lança um satélite de comunicação de 3.600 kg. Determine (a) a energia adicional necessária para pôr o satélite em uma
A força F = y z i + z x j + x y k / x y z age sobre uma partícula P x , y , z que se move no espaço. (a) Usando a relação deduzida no Problema 13.79 , mostre que essa força é uma força conservativa. (
A função potencial associada com a força P no espaço é conhecida por ser V x , y , z = - x 2 + y 2 + z 2 1 / 2 . (a) Determine os componentes x ,yez de P . (b) Calcule o trabalho feito por P de O para
Para a bola do Problema 13.93, determine (a) o menor valor admissível da velocidade inicial V A para que a corda permaneça esticada todo tempo, (b) a velocidade máxima correspondente alcançada pela bo