Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 64
A cavilha de madeira mostrada na figura é torneada para de diametro e de comprimento. Determine a porcentagem do volume inicial da cavilha que será desperdiçada.
Passo 1
Bom galera, o problema que que a gente diga em porcentagem o volume que vai ser perdido no torneamento.
Vamos começar, calculando o volume da cavilha, usando o teorema de Pappus-Guldinus, considerando que a cavilha é um solido de rotação da seguinte figura:
Onde, essa parte verde e vermelha são dadas por:
Ou seja, a área verde está cortada por um quarto de círculo e um arco de circulo está cortado por um triângulo de mesmo ângulo, vamos logo descobrir esse ângulo, é fácil, bem assim:
Usando a função inversa do seno na calculadora, a gente encontra:
Passo 2
Show de bola, agora a gente monta uma tabela pra encontrar o centroide em da figura:
Dica: O centroide de cada uma das figuras isoladas fica no final do livro.
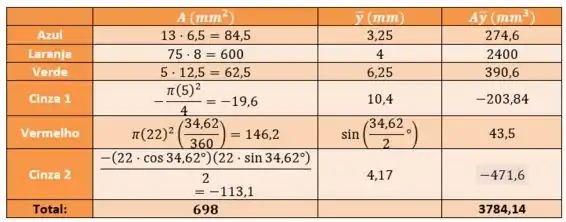
Passo 3
Então, o volume desse sólido é:
Agora, o volume depois de torneado:
Passo 4
Por fim, vamos calcular a porcentagem da diferença: