Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 105
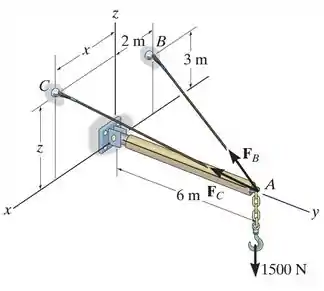
Dois cabos são usados para segurar o mastro guincho na posição e sustentar a carga de N. Se a força resultante é direcionada ao longo do mastro do ponto para , determine os valores de e para as coordenadas do ponto e a intensidade da força resultante. Considere N e N.
Passo 1
Nesse exercício sabemos a força resultante agirá apenas ao longo do eixo no sentido negativo.
Vamos começar encontrando as coordenadas dos pontos que definem a direção dos nossos vetores:
Definimos agora nossos vetores posição pelo ponto final menos inicial com seus devidos vetores unitários, assim:
Passo 2
Agora encontramos o módulo dos nossos vetores:
E então o vetor unitário que determina a direção e o sentido dos nossos vetores são:
Passo 3
Com isso, podemos expressar nossas forças como vetores cartesianos:
Passo 4
Sabemos que nossa força resultante é a soma de todas as forças:
E que essa agirá apenas no eixo , logo, nos outros eixos nossa resultante é zero, assim:
No eixo :
No eixo :
No eixo :
Passo 5
Agora trabalhamos nossas equações até descobrir as incógnitas, vamos dividir a equação pela equação :
E agora encontramos substituindo em :
Resolvendo isso obtemos:
Agora podemos encontrar substituindo nosso valor de na equação :
E finalmente substituímos nossos valores de e na equação para descobrir a força resultante: