Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 73
A lança leve em ângulo reto que sustenta o cilindro de é sustentada por três cabos e uma junta esférica em presa à superfície vertical -. Determine as reações em e as tensões nos cabos.
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar as reações no apoio em e as tensões nos cabos , e . Vamos começar fazendo o diagrama de corpo livre da lança com o seu peso, as reações em e as tensões dos cabos atuando nela.
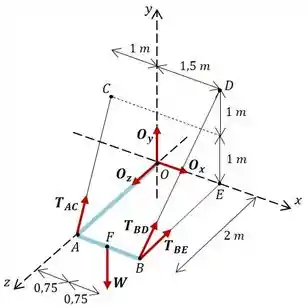
Show de bola, então bora começar definindo vetorialmente o peso do cilindro e as tensões nos cabos , e a partir de seus vetores unitários.
E para os cabos temos:
Passo 2
Muita conta né?
Calma que tudo vai dar certo no final! Hehehe Agora que temos todas as forças, vamos calcular o momento em torno do ponto , que deve ser nulo uma vez que o corpo está em equilíbrio.
Passo 3
Para que o somatório seja nulo, as componentes , e também devem ser nulas, então:
Da terceira equação temos:
Substituindo na primeira equação:
E, finalmente, substituindo e na segunda equação:
Com isso, temos as tensões nos cabos.
Passo 4
Para encontrar a reação em , vamos utilizar as equações de equilíbrio de forças nas direções , e :
Ufa! Essa foi graande hein? Agora partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 