Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 93

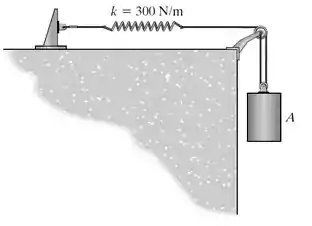
Quando o cilindro de 50 kg é solto do repouso, a mola é submetida a uma tração de 60 N. determine a velocidade do cilindro após ele ter caído 200 mm. Qual é a distância que ele caiu antes de parar instantaneamente ?

Passo 1

o comprimento da corda pode ser expressado de acordo com as coordenadas S A e S P como a figura abaixo mostra.

S P + 2 S A = l

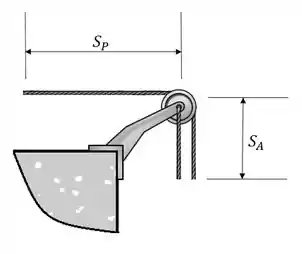
Sendo a suas varrições,

∆ S P + 2 ∆ S A = 0

Passo 2

A figura a seguir mostra as posições ( 1 ) e ( 2 ) e as deformações das molas para os deslocamentos do cilindro. A partir de cada estado é possível calcular as energias envolvida das no sistema.

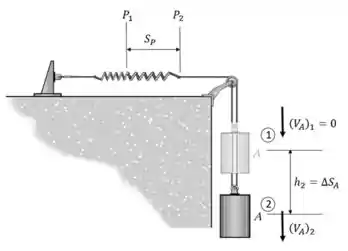
As energias potenciais gravitacionais para as posições ( 1 ) e ( 2 ) são,

E g 1 = m g h 1 = 50 9,81 0 = 0

E g 2 = m g h 2 = 50 9,81 - ∆ s A =   - 490,5 ∆ s A

Quando o cilindro vai da posição (1) para a posição (2), a deformação da moda é

s 1 = F k = 60 300 = 0,2   m  

E s 2 ,

s 2 = s 1 + ∆ s p = 0,2 + ∆ P m

Com as deformações s 1 e s 2 é possível calcular as energias potenciais elásticas

E e 1 = 1 2 k s 1 2 = 300 0,2 2 = 6   J  

E e 2 = 1 2 k s 2 2 = 300 0,2 + ∆ P 2 = 150 0,2 + ∆ P 2

Passo 3

Para o primeiro caso sendo ∆ s A = 0,2   m

∆ S P + 2 ( 0,2 ) = 0

∆ S P = - 0,4   m   o u   0,4   m   →

E C 1 + E g 1 +   E e 1   =   E C 2 + E g 2 +   E e 2  

1 2 m 0 2 + 0 + 6 =   1 2 m v 2 2   - 490,5 ∆ s A +   150 0,2 + ∆ P 2  

v 2 = 1,42   m / s

Para o caso que o cilindro está momentaneamente parado em ( 2 )

∆ S P =   - 2 ∆ s A

E v 2 = 0  

E C 1 + E g 1 +   E e 1   =   E C 2 + E g 2 +   E e 2  

0 + 0 + 6 = 0 - 490,5 ∆ s A +   150 0,2 + ∆ P 2  

∆ s A = 0,6175   m = 617,5   m m  

Resposta

A velocidade do cilindro após ele ter caído 200 mm é v 2 = 1,42   m / s e a distância que ele percorreu antes de parar foi 617,5   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espaçonave navega ao longo de uma trajetória parabólica em direção ao planeta Júpiter e a expectativa é de que atinja o ponto A com uma velocidade v A de intensidade 26,9k m / s . Seus motores ser
A melhor maneira de transferir um veículo espacial de uma órbita circular mais interna para uma outra órbita coplanar mais externa é acionando seus motores quando ele passar por A , a fim de aumentar
(a) Fazendo r = R + y no segundo membro à direita da E q .( 13.17 ’ ) e expandindo-o em uma série de potências de y R , mostre que a expressão na E q .( 13.16 ) para a energia potencial V g devido à g
Usando os princípios de conservação da energia e da quantidade de movimento angular, resolva o item a do Problema Resolvido 12.8.
Observações mostram que um corpo celeste que viaja a 1,9 × 10 6k m / h parece estar descrevendo um círculo em torno do ponto B de raio igual a 60 anos-luz. Suspeita-se que o ponto B seja uma concentra