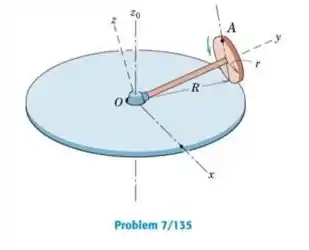
Determine a velocidade do ponto A sobre o disco do Prob. 7/135 para a posição mostrada.
Passo 1
Vamos tomar o ponto A que é o ponto de nosso interesse, e a origem dada na figura O, a relação de velocidade entre dois pontos é dada por:
Passo 2
Como a origem não se movimenta, , o produto vetorial será:
Onde é o ângulo formado entre a haste e o plano do disco maior (lembrando que no problema 135, a hipotenusa do triangulo retângulo não é a haste, ela é um dos catetos, mas sim o raio do disco maior, e r será o outro cateto).
E a velocidade relativa:
Sendo que pegamos do exercício 135.
Passo 3
Por fim, podemos calcular a velocidade do ponto A: