Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 91

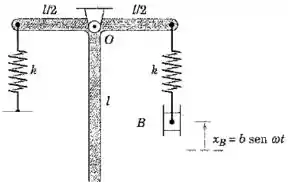
Duas barras uniformes e idênticas estão soldadas uma à outra em um ângulo reto e são articuladas em relação a um eixo horizontal que atravessa o ponto O como mostrado. Determine a frequência de excitação crítica ω c do bloco B , que resultará em oscilações excessivamente grandes do conjunto. A massa do conjunto soldado é m .

Passo 1

Já que a massa do conjunto é m , vamos considerar que cada um dos trechos (horizontal e vertical) tem massa m / 2 .

Além disso, podemos representar as forças que a mola e o compressor exercem quando o sistema está deslocado por um ângulo θ pequeno:

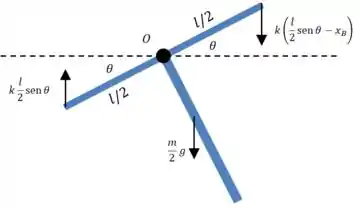
Perceba que o ponto O coincide com o centro de massa do trecho horizontal, por isso o seu peso terá momento nulo.

Agora podemos escrever uma equação de momentos em torno desse ponto:

∑ M O = M c o m p r + M m o l a + M p e s o

∑ M O = - k l 2 sen ⁡ θ l 2 cos ⁡ θ - k l 2 sen ⁡ θ - x B l 2 cos ⁡ θ - m g 2 l 2 sen ⁡ θ

Para simplificar a conta, vamos tirar proveito do fato de que as oscilações são pequenas, e então sen ⁡ θ ≅ θ e cos ⁡ θ ≅ 1 :

∑ M O = - k l 2 θ l 2 - k l 2 θ - x B l 2 - m g 2 l 2 θ

∑ M O = - l 2 k l 2 θ + k l 2 θ - x B + m g 2 θ

Passo 2

Agora vamos olhar para o outro lado da equação de momentos:

∑ M O = I O θ ¨

Precisamos calcular o momento de inércia em relação ao ponto O . Primeiro, temos uma barra vertical de massa m / 2 e comprimento l :

I 1 = 1 3 m 2 l 2 = 1 6 m l 2

Depois, temos duas barras de massa m / 4   cada e comprimento l / 2 :

I 2 = 2 1 3 m 4 l 2 2 = 1 24 m l 2

Então:

I O = I 1 + I 2 = 1 6 m l 2 + 1 24 m l 2

I O = 5 24 m l 2

Agora vamos substituir tudo na equação principal:

∑ M O = I O   θ ¨

- l 2 k l 2 θ + k l 2 θ - x B + m g 2 θ = 5 24 m l 2 θ ¨

Passo 3

Precisamos simplificar um pouco essa equação:

- k l 2 4 θ - k l 2 4 θ + k l x B 2 - m g l 4 θ = 5 24 m l 2 θ ¨

5 24 m l 2 θ ¨ + 1 2 k l 2 + 1 4 m g l θ = 1 2 k l x B

Vamos dividir tudo por 5 24 m l 2 :

θ ¨ + 12 5 k m + 6 5 g l θ = 12 5 k m l x B

E substituir a fórmula para x B que é dada no desenho do enunciado:

θ ¨ + 12 5 k m + 6 5 g l θ = 12 5 k m l b sen ⁡ ω t

Então, a frequência de excitação que estamos procurando é:

ω c 2 = 12 5 k m + 6 5 g l = 6 5 2 k m + g l

ω c = 6 5 2 k m + g l

Resposta

A frequência de excitação é ω c = 6 5 2 k m + g l .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

59. Cada uma das esferas de 0,5k g está presa à extremidade da haste elástica leve e se desloca de 4m m quando uma força de 2N é aplicada estaticamente à esfera. Se o cursor central recebe um moviment
62. A unidade motorizada de 20k g com velocidade variável é limitada na direção horizontal por duas molas, cada uma das quais possui uma rigidez de 2,1k N / m . Cada um dos dois amortecedores possui u
48. Determine a amplitude X do movimento em regime permanente da massa de 10k g se (a) c = 500N ⋅ s / m e(b) c = 0 .
61. O movimento do carrinho externo B é dado por x B = b ⋅ s e n ω t . Para qual faixa da frequência d excitação ω , a amplitude do movimento da massa m em relação ao carrinho é inferior a 2 b ?
96. O “boneco” segmentado do Prob. 6 / 107 é reapresentado aqui. Assume-se que articulação do quadril O permanece fica em relação ao carro, e o tronco acima do quadril é considerado como um corpo rígi