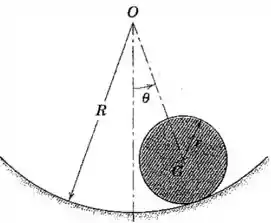
O cilindro maciço uniforme de massa e raio rola sem deslizar durante a sua oscilação sobre a superfície circular de raio . Se o movimento está limitado a pequenas amplitudes , determine o período das oscilações. Determine também a velocidade angular do cilindro quando cruza a linha de centro vertical. (Atenção: Não confunda com ou com conforme utilizado nas equações de definição. Observe também que não é o deslocamento angular do cilindro.)

Se aplicarmos a segunda lei de Newton na direção tangencial ao movimento de rotação do cilindro, ficaremos com a seguinte expressão:

Agora sim, podemos resolver o sistema de equações:

Dividimos a segunda equação por e somamos as duas equações:

E podemos aproximar , então:

Para resolver essa equação, preicamos escrever em função de .

Quando o cilindro vai um extremo ao outro da sua amplitude de oscilação, a distância que ele percorre é dada por:

Pensando em termos do ângulo pelo qual o cilindro gira em torno do próprio centro, temos:

Então:

E então:

Vamos substituir isso na nossa equação diferencial:

E então a frequência angular é:

E o período é:

Agora falta encontrar a velocidade angular no instante em que o cilindro passa pela linha de centro vertical.

Sabemos que, nesse ponto, tanto quanto são máximos, então:

Então vamos voltar à nossa equação diferencial de antes:

Que é simplesemten a equação do oscilador harmônico, cuja solução pode ser:

Vamos usar essa função para achar :

O valor máximo que essa função pode assumir (que acontece quando ) é:

Então:

Podemos simplificar essa equação da seguinte forma: