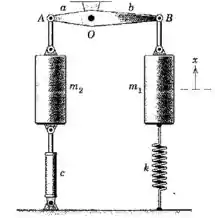
O sistema do Prob. 8/45 é repetido aqui. Se o elemento de ligação A B possui agora uma masssa m 3 e um raio de giração k O em relação ao ponto O , determine a equação do movimento em termos da variável x . Assuma pequenas oscilações. O coeficiente de amortecimento para o amortecedor é c .

A equação do movimento é m 1 + m 3 k o 2 b 2 + m 2 a 2 b 2 x ¨ + c a 2 b 2 x ˙ + k x = 0 .

Enunciado

Vamos começar aplicando as leis de Newton sobre cada uma das massas e na direção vertical:

Onde vamos chamar a coordenada vertical da massa de , e a da massa de .

Se a massa se desloca ligeiramente para cima, as forças que agem sobre ela serão as seguintes:

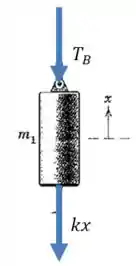
Então:

E uma situação semelhante acontece para a massa , mas ao invés de , a força no compressor é .

Como a massa se desloca ligeiramente para cima, a massa se desloca ligeiramente para baixo, daí a diferença no sinal de em relação a .

Então até aqui ficamos com duas equações:

E podemos montar também uma equação de momentos em torno do ponto :

Lembrando que estamos supondo que o sistema se inclina para a esquerda, de forma que a massa está descendo e a massa está subindo:

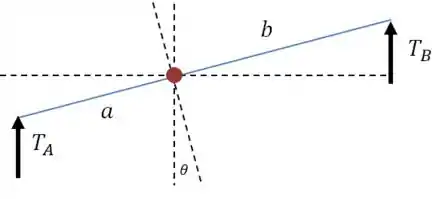
E o momento de inércia pode ser calculado através do raio de giração:

Então nosso sistema completo é:

Para poder resolver esse sistema, vamos escrever e em função de . Para isso vamos precisar de um desenho:

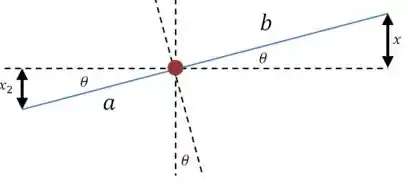
Olhando para a tangente do ângulo podemos escrever o seguinte:

E então:

E ainda olhando para o desenho, podemos relacionar e da seguinte forma:

Vamos substituir tudo isso no sistema:

E agora finalmente podemos resolver o sistema. Vamos multiplicar a primeira equação por e somar com a segunda:

Agora isolamos na segunda equação e substituímos nessa:

Agora é só reorganizar um pouco:

Dividundi tudo por :

Pronto, essa é a equação do movimento que estávamos procurando.

A equação do movimento é .