Determine a faixa de massas do cilindro na qual o sistema está em equilíbrio. Considere o caso em que o coeficiente de atrito entre o cabo e a superfície de apoio fixa vale 0,3. Inclua o atrito indicado entre o corpo de 100 kg e a rampa.
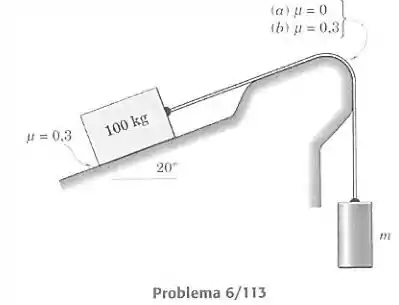
Passo 1
Nesse caso, há atrito entre a corda e a superfície, então a tração que é transmitida ao bloco pelo cabo é diferente do peso do cilindro . A fórmula para o equilíbrio do cabo nos dá a relação entre as trações nas duas extremidades do cabo:
Sendo a tração maior a tração menor, o coeficiente de atrito entre o cabo e a superfície e o ângulo total de contato do cabo com a superfície curva. O ângulo é igual a . Passando para radianos, obtemos:
Passando a equação para a forma exponencial, temos:
Agora vamos considerar os casos em que a força de atrito entre o bloco e o solo é estática para a esquerda e estática para a direita, que configuram nossos casos limites, os limiares de movimento do bloco.
Passo 2
- Bloco na iminência de descer. Nesse caso a tração é pequena e a força de atrito impede o bloco de descer. A força de atrito no cabo também impede ele de descer, então a tração menor é feita pelo peso do cilindro, e a tração maior é a tração no bloco. Achamos então em função de :
- Bloco na iminência de subir. Nesse caso a tração é grande, e o atrito impede o bloco de subir. Dessa vez o atrito no cabo feito pela superfície curva aponta para o outro lado, também impedindo o bloco de subir. Então a tração maior é feita pelo peso do cilindro, . Vamos então achar a tração no bloco. A configuração das outras forças é igual.
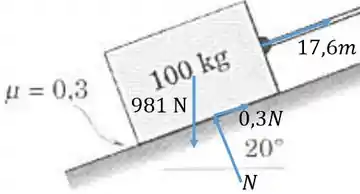
Vamos colocar o eixo paralelo à rampa e o eixo normal a ela. A inclinação do peso de 981 N em relação à normal é 20°. Vamos então às equações:
Passo 3
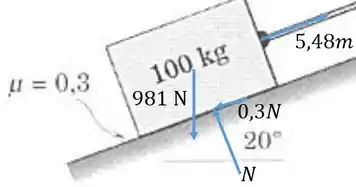
Então a massa do cilindro deve estar entre 3,36 kg e 112 kg.