Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 73
Um colar de 0,5 kg está preso a uma mola e desliza sem atrito ao longo de uma barra circular em um plano vertical. A mola tem um comprimento indeformado de 5 cm e uma constante k = 400 N/m. Sabendo que o colar está em equilíbrio em A e que recebe um leve impulso para se movimentar, determine a velocidade do colar e força normal entre o colar e a barra quando ele passar por B.
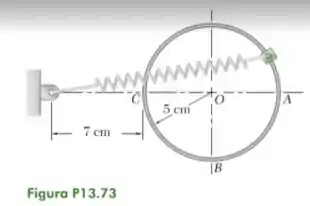
Fonte: Beer – Dinâmica – 9ª ed
Passo 1
Fala aí, tudo bem?
Bora pra mais uma?!
Bem, vamos analisar o problema de utilizando nossa amiga conservação de energia.
Façamos nossas considerações:
- Pelo enunciado, , ou seja, não há energia cinética;
- Vamos comparar os dois instantes: Em A e em B. Assim, usamos o ponto B como referencial, dessa forma, a energia potencial gravitacional nesse ponto é nula.
E inicialmente vamos fazer o cálculo de e para encontrar suas respectivas energias potenciais elásticas:
Em B:
Passo 2
Então, aplicando a conservação da energia entre os pontos, temos:
Substituindo os valores:
Assim:
Passo 3
Bem, para a força normal entre o colar e a barra façamos o diagrama de corpo livre em B:
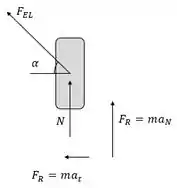
Onde
Então, pelo somatório de forças em y (detalhe para a igualdade :
Substituindo valores:
Então:
Resposta
Portanto:
E