Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 47

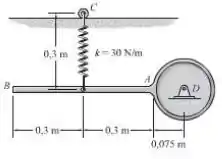
O pêndulo consiste de uma barra B A , de 2   k g , e um disco de 3   k g . A mola está deformada 0,09   m quando a barra está na horizontal, como mostrado. Se o pêndulo é solto do repouso e gira em torno do ponto D , determine sua velocidade angular no instante em que a barra se torna vertical. O rolete em C permite que a mola permaneça vertical quando a barra cai.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Podemos aplicar o princípio da conservação de energia analisando o momento incial e final do sistema.

A conservação de energia é dada por:

T 1 + V 1 = T 2 + V 2

Vamos analisar cada componente:

V 1 = 1 2 k x 1 2 + m g h 1

Considerando o ponto inicial h 1 = 0 , temos:

V 1 = 1 2 30 0,09 2

V 1 = 0,1215   N ⋅ m

Temos também que:

T 1 = 1 2 I G ω 1 2 + 1 2 m v 1 2

Como o sistema está em repouso no momento inicial, temos que v 1 e ω 1 são nulos, logo:

T 1 = 0

Passo 2

Para o momento final, temos:

V 2 = 1 2 k x 2 2 + m g h 2

Temos que h 2 = 0,3 + 0,075 = 0,375   m e como a orientação está para baixo, temos que definir como negativo. A deformação da mola será x 2 = 0,375 + 0,09 = 0,465   m . Portanto:

V 2 = 1 2 30 0,465 2 + 2 ( 9,81 ) ( - 0,375 )

V 2 = - 4,11   N ⋅ m

Para descobrir a parcela cinética, temos que encontrar os momentos de inércia da barra e do disco. Para a barra A B temos que aplicar o teorema dos eixos paralelos?.

I A B O = 1 12 m l 2 + m y - 2

E:

I D O = 1 2 M r D 2

Temos que:

I A B O = 1 12 2 0,6 2 + 2 0,375 2

I A B O = 0,34125

E:

I D O = 1 2 3 0,075 2

I D O = 0,0084375

A parcela cinética será:

T 2 = 1 2 I A B O ω 2 + 1 2 I D O ω 2

T 2 = 1 2 0,34125 ω 2 + 1 2 ( 0,00854375 ) ω 2

T 2 = 0,175 ω 2

Passo 3

Vamos aplicar conservação de energia:

T 1 + V 1 = T 2 + V 2

0 + 0,1215   = 0,175 ω 2 + ( - 4,11 )

ω = 4,92   r a d / s

Resposta

ω = 4,92   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A função potencial associada com a força P no espaço é conhecida por ser V x , y , z = - x 2 + y 2 + z 2 1 / 2 . (a) Determine os componentes x ,yez de P . (b) Calcule o trabalho feito por P de O para
Para a bola do Problema 13.93, determine (a) o menor valor admissível da velocidade inicial V A para que a corda permaneça esticada todo tempo, (b) a velocidade máxima correspondente alcançada pela bo
Uma espaçonave navega ao longo de uma trajetória parabólica em direção ao planeta Júpiter e a expectativa é de que atinja o ponto A com uma velocidade v A de intensidade 26,9k m / s . Seus motores ser
A melhor maneira de transferir um veículo espacial de uma órbita circular mais interna para uma outra órbita coplanar mais externa é acionando seus motores quando ele passar por A , a fim de aumentar
(a) Fazendo r = R + y no segundo membro à direita da E q .( 13.17 ’ ) e expandindo-o em uma série de potências de y R , mostre que a expressão na E q .( 13.16 ) para a energia potencial V g devido à g