Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 134
O comprimento do cabo AB é 20 m e a tensão neste cabo é 17350 N. Determine as componentes e da força exercida pelo cabo na âncora B, os ângulos e , definindo a direção e o sentido da força.
Passo 1
Vamos começar o exercício desenhando o DCL para o sistema:
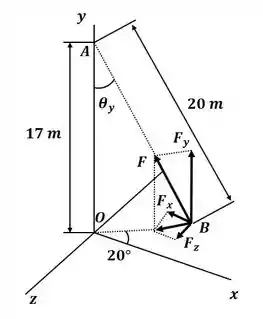
Agora vamos usar trigonometria no triângulo ABO para descobrir o valor de :
Passo 2
Agora vamos encontrar as componentes da força nas direções principais, começando por , temos:
Agora na direção :
E, por fim, na direção :
Passo 3
Agora, como já sabemos os valores das componentes em todas as direções e o enunciado nos deu o módulo total, podemos encontrar os ângulos principais através de:
Resposta
Exercícios de Livros Relacionados
A ponte Golden Gate em São Francisco tem um vão principal de 1280 m, uma deflexão de 143 m e um carregamento estático total de 310,8 kN por metro linear de medida horizontal. O peso de ambos os cabos
Medidas de deformação feitas nos cabos da ponte suspensa na posição A indicam um aumento da força trativa de 2,14 MN em cada um dos dois cabos principais devido ao recapeamento da ponte. Determine a m
Ache o comprimento total L da corrente que terá uma deflexão de 2 m quando for suspensa de dois pontos, distando de 10 m e situados sobre a mesma linha horizontal.
Repita o Prob. 5/155, mas não use a aproximação de um cabo parabólico. Compare seus resultados com a resposta dada para o Prob. 5/155.
Um cabo pesando 40 newtons por metro de comprimento está suspenso do ponto A e passa pela pequena polia em B. Determine a massa m do cilindro preso ao cabo, que vai produzir uma deflexão de 10 m. Devi