Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 135

No sentido de mover um caminhão acidentado, dois cabos foram fixados em A e puxados pelos guinchos B e C como mostrado na figura. Sabendo que a tração é 10 kN no cabo AB e 7,5 kN no cabo AC, determine a intensidade, direção e sentido da resultante das forças exercidas em A pelos dois cabos.

Passo 1

Vamos começar o exercício desenhando o DCL para o sistema:

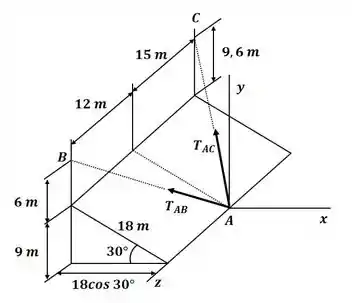
Agora precisamos escrever os vetores tensão em termos de suas coordenadas, para isso, precisamos primeiro escrever o vetor que liga esses pontos, então:

A B → = - 18 c o s 30 ° i → + 15 j → + 12 k → → A B → = - 15,59 i → + 15 j → + 12 k →

A C → = - 18 c o s 30 ° i → + 18,6 j → - 15 k → → A C → = - 15,59 i → + 18,6 j → - 15 k →

Agora, calculando o módulo desses vetores:

A B = - 15,59 2 + 15 2 + 12 2 → A B = 24,74   m

A C = - 15,59 2 + 18,6 2 + - 15 2 → A C = 28,53   m

Agora podemos escrever os vetores tensão como:

T → A B = T A B . A B → A B = 10 24,74 - 15,59 i → + 15 j → + 12 k → → T → A B = - 6,3 i → + 6,1 j → + 4,8 k →

T → A C = T A C . A C → A C = 7,5 28,53 - 15,59 i → + 18,6 j → - 15 k → → T → A C = - 4,1 i → + 4,9 j → - 3,9 k →

Passo 2

Agora vamos encontrar o vetor resultante no ponto A somando os dois vetores tensão encontrados no passo 1:

R → = T → A B + T → A C = - 6,3 i → + 6,1 j → + 4,8 k → + - 4,1 i → + 4,9 j → - 3,9 k →

R → = - 10,4 i → + 11 j → + 0,9 k →

Agora, calculando o módulo desse vetor, temos:

R = - 10,4 2 + 11 2 + 0,9 2 → R = 15,16   k N

Passo 3

Agora, como sabemos o valor de todas as componentes de R e o seu módulo, podemos encontrar os ângulos principais utilizando as relações a seguir:

cos ⁡ θ x = R x R = - 10,4 15,16 → θ x = 133,3 °

cos ⁡ θ y = R y R = 11 15,16 → θ y = 43,5 °

cos ⁡ θ z = R z R = 0,9 15,16 → θ z = 86,6 °

Resposta

R = 15,16   k N

θ x = 133,3 °

θ y = 43,5 °

θ z = 86,6 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma draga está ancorada em uma posição fixa por um único cabo-guia, que tem uma direção horizontal na fixação em A e percorre uma distância horizontal de 250 m até um ponto de ancoragem B em terra. Um
O planador A está sendo rebocado em um voo a altura constante e está 120 m atrás e 30 m abaixo do avião B. A tangente ao cabo no planador é horizontal. O cabo tem uma massa de 0,750 kg por metro de co
Um cabo sustenta uma carga uniformemente distribuída de 40 kg/m em relação à horizontal e está suspenso dos dois pontos fixos A e B, localizados como mostrado. Calcule as forças trativa nos cabos, em
Um tubo de água horizontal de 350 mm de diâmetro é sustentado sobre uma ravina pelo cabo mostrado. O tubo e a água dentro dele têm uma massa combinada de 1400 kg por metro de seu comprimento. Calcule
Calcule a força trativa T 0 no cabo, em A, necessária para sustentar a carga uniformemente distribuída em relação à horizontal. Determine também o ângulo θ feito pelo cabo com a horizontal, no ponto d