Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 91
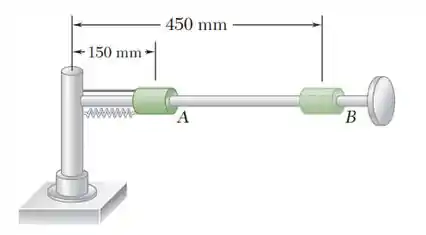
Considerando que a haste inicialmente gira a uma taxa de 12 rad /s, determine para a posição B do colar: (a) a componente transversal da velocidade do colar, (b) ascomponentes radial e transversal de sua aceleração, (c) a aceleraçãodo colar relativa à haste.
Passo 1
E ai gurizada tudo belezinha??? O enunciado pede que a gente determine a componente transversal da velocidade do colar, (b) as componentes radial e transversal de sua aceleração, (c) a aceleração do colar relativa à haste.
Primeiro notamos:
Em
Passo 2
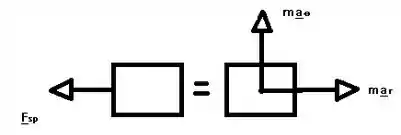
Depois que o cordão é cortado, a única força horizontal atuando no colar é devido à mola. Assim, o momento angular sobre o eixo é conservado.
=
Onde:
Então:
Passo 3
(b)Temos:
Passo 4
Passo 3
(C) Temos:
Agora:e
Então em B:
Resposta
a)
b)
c)
Exercícios de Livros Relacionados
O carrinho de massa 2 m é livre para se mover ao longo dos trilhos horizontais e transporta as duas esferas, cada uma com massa m , montadas sobre as hastes de comprimento l e massa desprezível. O eix
Os carros de um passeio de montanha-russa possuem uma velocidade de 30k m / h quando passam pelo topo do trilho circular. Despreze qualquer atrito e calcule suas velocidades v quando atingem a posição
O pequeno carro, que possui uma massa de 20k g , se desloca livremente sobre o trilho horizontal e transporta a esfera de 5k g montada na haste leve que está girando com r = 0,4m . Uma unidade motora
As duas pequenas esferas, cada uma com massa m , estão conectadas por um cordão de comprimento 2 b (medido até os centros das esferas) e estão inicialmente em repouso sobre uma superfície horizontal l
Uma corda flexível inextensível de massa ρ por unidade de comprimento e comprimento igual a 1 / 4 da circunferência do tambor fixo de raio r é liberada a partir do repouso na posição horizontal tracej