Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 10

Se a corda é submetida a uma força horizontal P = 150 N, e a engrenagem está suportada por um pino fixo em O, determine a velocidade angular da engrenagem e a velocidade da cremalheira de 20 kg em 4 s, partindo do repouso. A massa da engrenagem é 50 kg e ela tem um raio de giração k O = 125   m m . Suponha que a superfície de contato entre a cremalheira e o plano horizontal é lisa.

Passo 1

Começaremos calculando o momento de inércia da engrenagem através de seu raio de giração:

I O = m k O 2 = 50 0,125 2 = 0,78125   k g . m 2

Como o enunciado nos forneceu, a engrenagem gira em torno de um ponto fixo e podemos relacionar sua velocidade angular com a velocidade linear da cremalheira da seguinte forma:

v O = ω r = ω ( 0,15 )

Passo 2

Agora podemos aplicar o princípio do impulso e da quantidade de movimento angular com o auxílio da imagem a seguir que possui os diagramas da engrenagem e da cremalheira:

↺ +   I O ω 1 + ∑ ∫ t 1 t 2 M O d t = I O ω 2

0 + F 4 0,15 - 150 4 0,075 = - 0,78125 ω

F = 75 - 1,302 ω

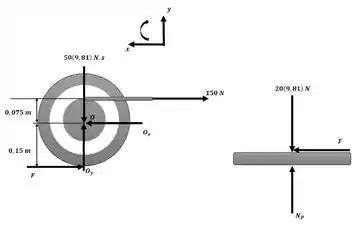
Essa será nossa equação número 1. Podemos ainda aplicar o princípio do impulso e da quantidade de movimento na direção x:

+ ←   m v 1 + ∑ ∫ t 1 t 2 F x d t = m v 2

0 + F 4 = 20 ω 0,15

F = 0,75 ω

Essa será nossa equação número 2.

Passo 3

Agora iremos igualar as equações 1 e 2 para descobrir o valor de ω :

75 - 1,302 ω = 0,75 ω

ω = 36,5   r a d / s

Por fim, podemos descobrir a velocidade linear da cremalheira através da equação proposta no passo 1:

v O = ω r = ( 36,5 ) ( 0,15 )

v O = 5,48   m / s

Resposta

ω = 36,5   r a d / s

v O = 5,48   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O rotor maior tem uma massa de 60k g e um raio de giração em relação ao seu eixo vertical de 200m m . O rotor menor é um disco circular maciço com uma massa de 8k g e está inicialmente girando com uma
A roda de 10k g tem um diâmetro de 400m m e um raio de giração em relação ao seu eixo de 180m m . A roda carrega um eixo com 4k g , de pequeno diâmetro, através do seu centro como mostrado. Se a roda
Uma barra esbelta uniforme de massa M e comprimento L está em translação sobre o plano horizontal liso x - y com uma velocidade de v M quando uma partícula de massa m , que se desloca com uma velocida
Determine a quantidade de movimento angular da Terra em relação ao centro do Sol. Suponha a Terra homogênea e uma órbita circular da Terra com raio 149,6 10 6k m ; consulte a Tabela D/2 para outras in
A barra esbelta de massa m e comprimento b é articulada na sua extremidade inferior em O , na forma mostrada no detalhe separado do suporte O . A barra é liberada a partir do repouso na posição vertic