Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 78

Determine a frequência natural f n para pequenas oscilações no plano vertical em torno do mancal O para o disco semicircular de raio r .

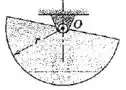
Passo 1

Vamos começar montando uma equação de momentos em torno do ponto O :

∑ M O = I O θ ¨

A única força que produz momento em torno desse ponto é o peso do disco. Então:

∑ M O = - m g sen ⁡ θ r -

Onde r - é a distância entre o ponto O e o centro de massa do disco. Esse valor pode ser consultado em uma tabela:

r - = 4 r 3 π

Então:

∑ M O = - 4 m r g 3 π sen ⁡ θ

Passo 2

Agora vamos olhar para o outro lado da equação:

∑ M O = I O θ ¨

O momento de inércia I O do disco em relação ao ponto O também é tabelado:

I O = 1 2 m r 2

Então:

- 4 m r g 3 π sen ⁡ θ = 1 2 m r 2 θ ¨

Para pequenas oscilações, podemos aproximar sen ⁡ θ ≅ θ :

- 4 m r g 3 π θ = 1 2 m r 2 θ ¨

Então:

θ ¨ + 8 g 3 π r θ = 0

O termo que está multiplicando θ é o quadrado da frequência natural do oscilador, então:

ω n = 8 g 3 π r

Mas queremos calcular a frequência f n , e não a frequência angular, então vamos lembrar da seguinte relação:

f n = ω n 2 π

f n = 1 2 π 8 g 3 π r = 1 π 2 g 3 π r

Resposta

A frequência natural para pequenas oscilações é 1 π 2 g 3 π r .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

61. Uma força propulsora variando senoidalmente é aplicada a um oscilador harmônico amortecido. a ) Quais são as unidades da constante de amortecimento b ? b ) Mostre que a grandeza k m possui as mesm
Um oscilador não amortecido de massa m e frequência própria ω 0 move-se sob a ação de uma força externa F = F 0 exp ⁡ - β t , onde β0 é uma constante. Inicialmente, o oscilador encontra-se em repouso
Para um oscilador de massa m , frequência livre ω 0 e constante de amortecimento γ , sujeito à força externa F = F 0 cos ⁡ ω t , calcule: (a) O valor exato de ω para o qual a amplitude de oscilação es
Seja x = a cos ⁡ ω t + b sen ⁡ ω t a solução estacionária para o movimento de um oscilador amortecido sob a ação da força F = F 0 cos ⁡ ω t . Mostre que somente a componente em quadratura contribui pa
Duas partículas de mesma massa, igual a 250g , estão suspensas do teto por barras idênticas, de 0,5m de comprimento e massa desprezível, e estão ligadas uma à outra por uma mola de constante elástica