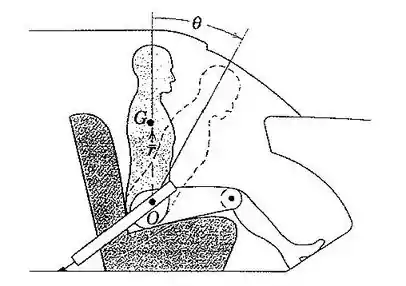
96. O “boneco” segmentado do Prob. é reapresentado aqui. Assume-se que articulação do quadril permanece fica em relação ao carro, e o tronco acima do quadril é considerado como um corpo rígido de massa . O centro de massa do tronco está em e o raio de giração do tronco em relação a é . Assuma que a resposta muscular atua como uma mola de torção interna que exerce um momento sobre a parte superior do tronco, onde é a constante de mola tradicional e é o deslocamento angular a partir da posição vertical inicial. Se o carro é forçado a uma parada súbita com um a desaceleração constante , desenvolva a equação diferencial para o movimento do tronco antes do seu impacto com o painel.
Passo 1
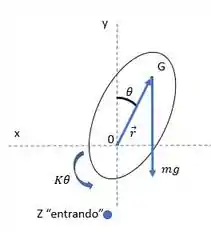
Primeiro, vamos montar o diagrama de corpo livre do boneco:
Passo 2
Agora que temos o esquema de forças no boneco, bora fazer a somatória de momentos. (Vamos utilizar a barra embaixo para indicar que é um vetor quando em cima já tiver uma notação, como por exemplo, a derivação em relação ao tempo):
Sabemos que
E podemos observar que e
Se fizermos o produto vetorial (, vamos encontrar:
Substituindo todas as equações, temos:
Resposta
A equação para o movimento do tronco será: